| Codeforces Round 211 (Div. 2) |
|---|
| Закончено |
Пусть задана таблица n × m, заполненная целыми числами. Клетку в i-ой строке и j-ом столбце будем обозначать (i, j). Таким образом, (1, 1) является левой верхней клеткой таблицы, а (n, m) — правой нижней. Назовем кругом радиуса r с центром в клетке (i0, j0) множество таких клеток (i, j), что 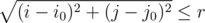 . Будем рассматривать только такие круги, которые не выходят за пределы таблицы, то есть у которых r + 1 ≤ i0 ≤ n - r и r + 1 ≤ j0 ≤ m - r.
. Будем рассматривать только такие круги, которые не выходят за пределы таблицы, то есть у которых r + 1 ≤ i0 ≤ n - r и r + 1 ≤ j0 ≤ m - r.
 Круг радиуса 3 с центром в (4, 5).
Круг радиуса 3 с центром в (4, 5). Найдите два таких непересекающихся круга заданного радиуса r, что сумма чисел в клетках, принадлежащим этим кругам, максимальна. Два круга пересекаются, если найдется клетка, принадлежащая обоим кругам. Поскольку может быть более одного способа выбрать пару кругов с максимальной суммой, то нас будет интересовать еще и количество таких пар. Посчитайте количество неупорядоченных пар кругов, то есть, к примеру, пара кругов радиуса 2 с центрами в (3, 4) и (7, 7) это та же самая пара, что и пара кругов радиуса 2 с центрами в (7, 7) и (3, 4).
В первой строке записано три целых числа n, m и r (2 ≤ n, m ≤ 500, r ≥ 0). Каждая из следующих n строк содержит по m целых чисел в диапазоне от 1 до 1000 — элементы таблицы. Строки таблицы перечислены сверху вниз, элементы в строках — слева направо. Гарантируется, что существует хотя бы один круг радиуса r, не выходящий за пределы таблицы.
Выведите два числа — максимальную сумму чисел в клетках, которые находятся в двух непересекающихся кругах, и количество пар непересекающихся кругов с максимальной суммой. Если не существует ни одной пары непересекающихся кругов, то выведите 0 0.
2 2 0
1 2
2 4
6 2
5 6 1
4 2 1 3 2 6
2 3 2 4 7 2
5 2 2 1 1 3
1 4 3 3 6 4
5 1 4 2 3 2
34 3
3 3 1
1 2 3
4 5 6
7 8 9
0 0
| Название |
|---|




