A. Таблица
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
stdin
вывод
stdout

У Семена есть прямоугольная таблица, состоящая из n строк и m столбцов. Семен пронумеровал строки таблицы, начиная от единицы, сверху вниз, а столбцы — начиная от единицы, слева направо. Ячейку, расположенную на пересечении x-ой строки и y-ого столбца, будем обозначать парой чисел (x, y). Углами таблицы будем называть ячейки: (1, 1), (n, 1), (1, m), (n, m).

Семен считает, что в этой таблице некоторые ячейки являются хорошими. Причем известно, что ни одна хорошая ячейка не является углом таблицы.

Изначально все ячейки таблицы бесцветны. Семен хочет покрасить все ячейки своей таблицы. За один ход он может выбрать любую хорошую ячейку таблицы (x1, y1), произвольный угол таблицы (x2, y2) и закрасить все ячейки таблицы (p, q), для которых выполняются оба неравенства: min(x1, x2) ≤ p ≤ max(x1, x2), min(y1, y2) ≤ q ≤ max(y1, y2).

Помогите Семену! Определите минимальное количество операций, необходимых ему для покраски всех ячеек таблицы. Обратите внимание, что одну ячейку разрешается покрасить несколько раз.

Входные данные

В первой строке заданы ровно два целых числа n, m (3 ≤ n, m ≤ 50).

Далее в n строках задано описание ячеек таблицы. А именно, в i-ой строке задано m целых чисел через пробел ai1, ai2, ..., aim. Если aij равно нулю, то ячейка (i, j) не является хорошей, иначе — aij равно единице. Гарантируется, что хотя бы одна ячейка является хорошей. Гарантируется, что ни одна хорошая ячейка не является углом.

Выходные данные

Выведите единственное число — минимальное количество операций, необходимых Семену для осуществления его затей.

Примеры
Входные данные
3 3
0 0 0
0 1 0
0 0 0
Выходные данные
4
Входные данные
4 3
0 0 0
0 0 1
1 0 0
0 0 0
Выходные данные
2
Примечание

В первом примере последовательность операций может быть такой:

  • В первый раз нужно выбрать ячейку (2, 2) и угол (1, 1).
  • Во второй раз нужно выбрать ячейку (2, 2) и угол (3, 3).
  • В третий раз нужно выбрать ячейку (2, 2) и угол (3, 1).
  • В четвертый раз нужно выбрать ячейку (2, 2) и угол (1, 3).

В втором примере последовательность операций может быть такой:

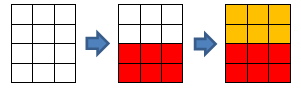
  • В первый раз нужно выбрать ячейку (3, 1) и угол (4, 3).
  • Во второй раз нужно выбрать ячейку (2, 3) и угол (1, 1).