За тридевять земель, за тридевять морей есть графство и королевство на берегу реки. В один день граф графства и король королевства решили, что земли у них не очень много, и было бы здорово превратить часть реки в землю.
Река представлена сеткой из r строк и ровно двух столбцов. Каждая ячейка сетки представляет собой прямоугольный участок реки. Строки пронумерованы от 1 до r сверху вниз, а столбцы от 1 до 2 слева направо.
В начале все ячейки сетки заняты рекой. Граф и Король планируют превратить некоторые ячейки с рекой в землю. Каждый по очереди будет выбирать одну ячейку, превращать ее в землю и присоединять к своим владениям.
Однако, по реке пролегает очень важный торговый маршрут. Граф и Король должны поддерживать реку так, чтобы корабли могли по прежнему проплыть от одного конца реки до другого. Иными словами, если ячейка (r, c) была превращена в землю, нельзя превращать в землю ячейки (r - 1, 3 - c), (r, 3 - c) и (r + 1, 3 - c).
Король и Граф не дружат друг с другом, и поэтому оба хотят быть последним, кто превратит ячейку реки в землю (им не важно сколько каждый из них превратит ячеек, важно только кто превратит ячейку в землю последний). К текущему моменту граф и король уже превратили n ячеек в землю. Ваша задача определить, кто в конечном итоге превратит ячейку с морем в землю последним, если известно, что, начиная с текущего момента игры, оба выбирают ячейки оптимально.
Первая строка содержит два целых числа r и n (1 ≤ r ≤ 100, 0 ≤ n ≤ r). Затем следуют n строк, описывающих уже превращенные ячейки. Каждая строка содержит два целых числа: ri и ci (1 ≤ ri ≤ r, 1 ≤ ci ≤ 2), что означает, что ячейка в строке ri и столбце ci уже превращена в землю. Все перечисленные ячейки попарно различны, и не перекрывают торговый маршрут.
Выведите «WIN» если правитель, который делает превращение первым, гарантированно будет последним, кто превратит ячейку из реки в землю. Иначе, выведите «LOSE».
3 1
1 1
WIN
12 2
4 1
8 1
WIN
1 1
1 2
LOSE
В первом примере есть 3 возможных хода для первого правителя: (2, 1), (3, 1) и (3, 2). Первые два хода заведомо проигрышные, так как оставляют ровно одну ячейку, которую можно превратить, для второго правителя.
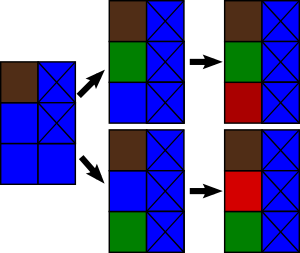
Однако, превращение (3, 2) не оставляет ячеек, которые можно превращать, поэтому первый правитель побеждает.
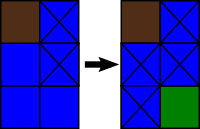
В третьем примере нет ячеек, которые можно превратить в землю.
| Название |
|---|




