| Codeforces Round 192 (Div. 1) |
|---|
| Закончено |
Дан неориентированный граф, состоящий из n вершин, пронумерованных от 1 до n. У каждой вершины есть не более двух инцидентных ребер. Для каждой пары вершин существует не более одного соединяющего их ребра. Ни одно ребро не соединяет вершину с самой собой.
Мне хотелось бы построить новый граф таким образом, чтобы:
- Новый граф состоял из такого же количества вершин и ребер, что и старый граф.
- Свойства, указанные в первом абзаце, выполнялись.
- Для каждых двух вершин u и v, если в старом графе есть соединяющее их ребро, то в новом графе соединяющего их ребра нет.
Помогите мне построить новый граф.
Первая строка содержит два целых числа через пробел, n и m (1 ≤ m ≤ n ≤ 105), обозначающих количество вершин и ребер, соответственно. Далее следуют m строк. Каждая из m строк состоит из двух разделенных пробелом целых чисел u и v (1 ≤ u, v ≤ n; u ≠ v), обозначающих ребро между вершинами u и v.
Если построить новый граф с упомянутыми выше свойствами невозможно, то выведите в единственной строке -1. В противном случае выведите ровно m строк. Каждая строка должна описывать ребро в формате, указанном во входных данных.
8 7
1 2
2 3
4 5
5 6
6 8
8 7
7 4
1 4
4 6
1 6
2 7
7 5
8 5
2 8
3 2
1 2
2 3
-1
5 4
1 2
2 3
3 4
4 1
1 3
3 5
5 2
2 4
Старый граф из первого примера:
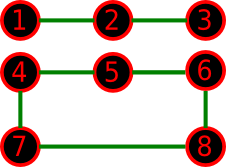
Возможный новый граф для первого примера:
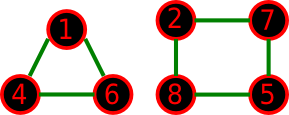
Во втором примере мы не можем построить новый граф, удовлетворяющий ограничениям.
Старый граф из третьего примера:
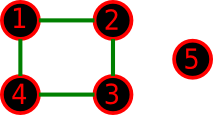
Возможный новый граф для третьего примера:

| Название |
|---|




