| Codeforces Round 183 (Div. 1) |
|---|
| Закончено |
Дана прямоугольная сетка размера n × m. Введем систему координат на сетке. Итак, каждая точка на сетке имеет координаты — пару целых чисел (x, y) (0 ≤ x ≤ n, 0 ≤ y ≤ m).
Ваша задача — найти наибольший подпрямоугольник на сетке (x1, y1, x2, y2), содержащий данную точку (x, y), такой, что соотношение длин его сторон равняется (a, b). Иными словами, должны выполняться следующие условия: 0 ≤ x1 ≤ x ≤ x2 ≤ n, 0 ≤ y1 ≤ y ≤ y2 ≤ m, 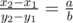 .
.
Стороны этого подпрямоугольника должны быть параллельны осям координат. Величины x1, y1, x2, y2 должны быть целыми.
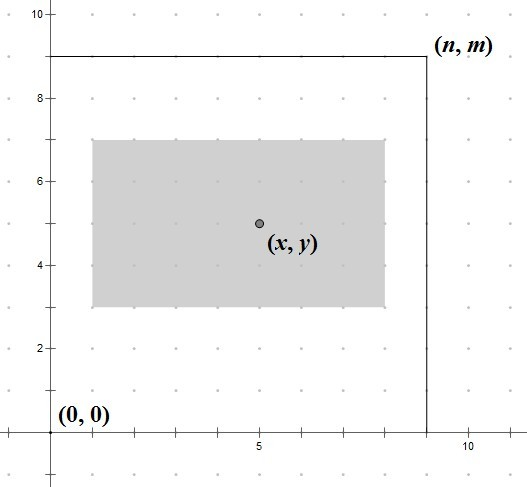
Если существует несколько ответов, найдите ближайший к (x, y) подпрямоугольник. Здесь «ближайший» означает, что Евклидово расстояние между (x, y) и центром прямоугольника как можно меньше. Если все равно существует несколько ответов, выведите лексикографически минимальный. Здесь «лексикографически минимальный» означает, что мы должны рассматривать подпрямоугольник как последовательность целых чисел (x1, y1, x2, y2), так, что можно выбрать из них лексикографически минимальную.
В первой строке записано шесть целых чисел n, m, x, y, a, b (1 ≤ n, m ≤ 109, 0 ≤ x ≤ n, 0 ≤ y ≤ m, 1 ≤ a ≤ n, 1 ≤ b ≤ m).
Выведите четыре целых числа x1, y1, x2, y2, обозначающие обнаруженный вложенный прямоугольник с левым нижним углом в (x1, y1), а правым верхним — в (x2, y2).
9 9 5 5 2 1
1 3 9 7
100 100 52 50 46 56
17 8 86 92
| Название |
|---|




