| Codeforces Round 150 (Div. 1) |
|---|
| Закончено |
Однажды Петя на день рождения получил в подарок от мамы книжку «Легенды и Мифы Теории Графов». Оттуда он узнал о таком графе как гидра.
Неориентированный граф называется гидрой, если он имеет структуру, указанную на рисунке ниже. А именно: имеются две соединенные ребром вершины u и v, которые соответственно называются грудью и животом гидры. Грудь соединена с h вершинами, которые называются головами гидры. Живот соединен с t вершинами, которые называются хвостами гидры. Заметим, что гидра является деревом, состоящим из h + t + 2 вершин.
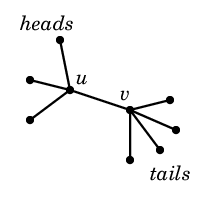
Еще у Пети есть неориентированный граф G, состоящий из n вершин и m ребер, который он получил в подарок от мамы на прошлый день рождения. Граф G не содержит петель и кратных ребер.
Теперь Петя хочет найти в графе G какую-нибудь гидру. Или же установить, что там гидры не содержится.
В первой строке записаны четыре целых числа n, m, h, t (1 ≤ n, m ≤ 105, 1 ≤ h, t ≤ 100) — количество вершин и ребер графа G, а так же количество голов и хвостов у гидры.
В следующих m строках дано описание ребер графа G. В i-ой из этих строк записаны два целых числа ai и bi (1 ≤ ai, bi ≤ n, a ≠ b) — номера вершин, которые соединяет i-ое ребро.
Гарантируется, что граф G не содержит петель и кратных ребер. Считайте, что вершины графа G пронумерованы целыми числами от 1 до n.
Если в графе G гидры нет, то выведите «NO» (без кавычек).
Иначе в первой строке выведите «YES» (без кавычек). Во второй строке выведите два целых числа — номера вершин u и v. В третьей строке выведите h чисел — номера вершин, которые являются головами. В четверной строке выведите t чисел — номера вершин, которые являются хвостами. Все выведенные вершины должны быть различны.
Если возможных ответов несколько — разрешается вывести любой.
9 12 2 3
1 2
2 3
1 3
1 4
2 5
4 5
4 6
6 5
6 7
7 5
8 7
9 1
YES
4 1
5 6
9 3 2
7 10 3 3
1 2
2 3
1 3
1 4
2 5
4 5
4 6
6 5
6 7
7 5
NO
На картинке ниже изображен первый тестовый пример:
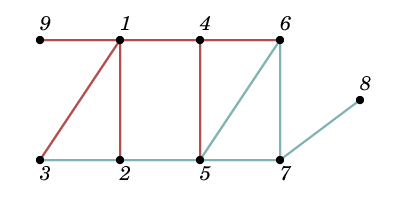
| Название |
|---|




