| Codeforces Round 147 (Div. 2) |
|---|
| Закончено |
Вам задано неориентированное дерево s, состоящее из n вершин. Необходимо построить для него оптимальную Д-декомпозицию. Определим Д-декомпозицию следующим образом.
Обозначим за v множество всех вершин s. Рассмотрим неориентированное дерево t, вершинами которого являются некоторые непустые подмножества v, которые обозначим через xi 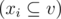 . Дерево t является Д-декомпозицией s, если выполняются следующие условия:
. Дерево t является Д-декомпозицией s, если выполняются следующие условия:
- объединение всех xi равно v;
- для любого ребра (a, b) дерева s существует вершина дерева t, содержащая как a, так и b;
- если вершины дерева t xi и xj, содержат вершину a дерева s, то все вершины дерева t, лежащие на пути из xi в xj также содержат вершину a, то есть это условие эквивалентно тому, что все вершины дерева t, которые содержат вершину a дерева s, образуют связное поддерево дерева t.
Очевидно, что существует много различных деревьев t, являющихся Д-декомпозициями дерева s. Например, Д-декомпозицией является дерево, состоящее из одной вершины, представляющей собой все множество v.
Назовем мощностью вершины xi количество вершин дерева s, которые в ней содержатся. Выберем в дереве t вершину с максимальной мощностью. Пусть ее мощность равна w. Тогда весом Д-декомпозиции t назовем величину w. Оптимальной назовем Д-декомпозицию, у которой вес минимален.
Вам необходимо найти оптимальную Д-декомпозицию, заданного дерева s имеющую наименьшее количество вершин.
В первой строке задано единственное целое число n (2 ≤ n ≤ 105), обозначающее количество вершин в дереве s.
В каждой из следующих n - 1 строк через пробел заданы два целых числа ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi), обозначающие, что вершины дерева s с номерами ai и bi соединены ребром.
Считайте, что вершины дерева s пронумерованы от 1 до n. Гарантируется, что s является деревом.
В первой строке выведите единственное целое число m, обозначающее количество вершин в искомой Д-декомпозиции.
Далее выведите m строк, содержащих описания вершин Д-декомпозиции. В i-той (1 ≤ i ≤ m) из них выведите описание вершины xi Д-декомпозиции. Описание каждой из вершин xi должно начинаться с целого числа ki, обозначающего количество вершин исходного дерева s, которые содержатся в вершине xi. Далее через пробел нужно вывести ki различных целых чисел — номера вершин из s, содержащихся в xi, в любом порядке.
Далее выведите m - 1 строк, содержащих по два целых числа pi, qi (1 ≤ pi, qi ≤ m; pi ≠ qi). Пара чисел pi, qi обозначает наличие ребра между вершинами xpi и xqi Д-декомпозиции.
Выведенная Д-декомпозиция должна быть оптимальной Д-декомпозицией для заданного дерева s и содержать минимально возможное количество вершин среди оптимальных. Если существует несколько оптимальных Д-декомпозиций с минимальным количеством вершин, выведите любую из них.
2
1 2
1
2 1 2
3
1 2
2 3
2
2 1 2
2 2 3
1 2
4
2 1
3 1
4 1
3
2 2 1
2 3 1
2 4 1
1 2
2 3
| Название |
|---|




