| Codeforces Round 126 (Div. 2) |
|---|
| Закончено |
Пока большинство студентов все еще сдает экзамены, в тракторном институте сессия уже завершилась. В этом институте студенты изучают всего одну дисциплину — искусство тракторного дела. Поэтому за целую сессию в зачетку студента ставится всего одна оценка — тройка, четверка или пятерка. Двоечников, к сожалению, отчисляют.
В институте учится n студентов, и, как ни странно, каждый из них может получать стипендию. Каждый семестр размер стипендии меняется. Поскольку сессия толька завершилась, то самое время определить размер стипендии до конца следующего семестра.
Месячный бюджет стипендии тракторного института составляет s рублей. Чтобы распределить этот бюджет оптимально, необходимо придерживаться следующих правил:
- Студенты, получившие одинаковые оценки за сессию, должны получать одинаковую стипендию;
- Обозначим размер стипендии (в рублях) студентов, получивших оценки 3, 4 и 5 за экзамен, k3, k4 и k5 соответственно. Величины k3, k4 и k5 должны быть целыми числами и удовлетворять неравенствам 0 ≤ k3 ≤ k4 ≤ k5;
- Пусть c3, c4, c5 — количество студентов, получивших оценку за сессию 3, 4 и 5 соответственно. Бюджет стипендии нужно потратить полностью, то есть c3·k3 + c4·k4 + c5·k5 = s;
- Введем функцию
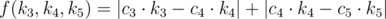 — величину, показывающую насколько хорошо распределена стипендия между студентами. В оптимальном распределении функция f(k3, k4, k5) принимает минимально возможное значение.
— величину, показывающую насколько хорошо распределена стипендия между студентами. В оптимальном распределении функция f(k3, k4, k5) принимает минимально возможное значение.
Зная результаты сессии и размер бюджета s, от Вас требуется найти оптимальное распределение стипендии.
В первой строке заданы два целых числа n, s (3 ≤ n ≤ 300, 1 ≤ s ≤ 3·105) — количество студентов и размер бюджета стипендии соответственно. Во второй строке задано n целых чисел, где i-ое число означает оценку за экзамен i-го студента. Гарантируется, что каждую оценку получил хотя бы один студент.
В единственной строке выведите три целых числа k3, k4 и k5 — искомые величины, обозначающие оптимальное распределение размеров стипендии. Если оптимальных ответов несколько, выведите любой из них. Если ответа не существует, выведите -1.
5 11
3 4 3 5 5
1 3 3
6 15
5 3 3 4 4 5
-1
| Название |
|---|




