Это сложная версия задачи. Разница между простой и сложной версиями задачи заключается только в допустимых символах в $$$s$$$. Вы можете делать взломы только в том случае, если обе версии задачи решены.
Дана перестановка $$$p$$$ длины $$$n$$$. Также дана строка $$$s$$$ длины $$$n$$$, содержащая только символы L, R и ?.
Для каждого $$$i$$$ от $$$1$$$ до $$$n$$$:
- Определим $$$l_i$$$ как наибольший индекс $$$j < i$$$ такой, что $$$p_j > p_i$$$. Если такого индекса не существует, $$$l_i := i$$$.
- Определим $$$r_i$$$ как наименьший индекс $$$j > i$$$ такой, что $$$p_j > p_i$$$. Если такого индекса не существует, $$$r_i := i$$$.
Изначально есть неориентированный граф с $$$n$$$ вершинами (пронумерованными от $$$1$$$ до $$$n$$$) и без рёбер. Затем для каждого $$$i$$$ от $$$1$$$ до $$$n$$$ в граф добавляется одно ребро:
- Если $$$s_i =$$$ L, в граф добавляется ребро $$$(i, l_i)$$$.
- Если $$$s_i =$$$ R, в граф добавляется ребро $$$(i, r_i)$$$.
- Если $$$s_i =$$$ ?, в граф добавляется либо ребро $$$(i, l_i)$$$, либо ребро $$$(i, r_i)$$$ по вашему выбору.
Найдите максимально возможный диаметр$$$^{\text{∗}}$$$ среди всех связных графов, которые вы можете получить. Выведите $$$-1$$$, если невозможно получить ни один связный граф.
$$$^{\text{∗}}$$$ Пусть $$$d(s, t)$$$ это наименьшее возможное число рёбер на пути от $$$s$$$ до $$$t$$$.
Диаметр графа определяется как наибольшее значение $$$d(s, t)$$$ по всем парам вершин $$$s$$$ и $$$t$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 2 \cdot 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 4 \cdot 10^5$$$) — длину перестановки $$$p$$$.
Вторая строка каждого набора входных данных содержит $$$n$$$ различных целых чисел $$$p_1,p_2,\ldots, p_n$$$ ($$$1 \le p_i \le n$$$) — элементы $$$p$$$, которые гарантированно являются перестановкой.
Третья строка каждого набора входных данных содержит строку $$$s$$$ длины $$$n$$$. Гарантируется, что строка состоит только из символов L, R и ?.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$4 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — максимальный диаметр среди всех связных графов, которые вы можете получить, или $$$-1$$$, если таковых нет.
852 1 4 3 5R?RL?21 2LR33 1 2L?R75 3 1 6 4 2 7?R?R?R?55 2 1 3 4?????66 2 3 4 5 1?LLRLL81 7 5 6 2 8 4 3?R??????126 10 7 1 8 5 12 2 11 3 4 9????????????
3 -1 -1 4 4 3 5 8
В первом наборе входных данных можно получить два связных графа (в вершинах написаны индексы):
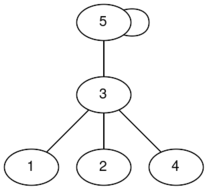 | 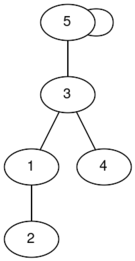 |
У графа слева диаметр равен $$$2$$$, а у графа справа диаметр равен $$$3$$$, поэтому ответ $$$3$$$.
Во втором наборе входных данных нельзя получить связный граф, поэтому ответ $$$-1$$$.
| Название |
|---|




