| Codeforces Round 946 (Div. 3) |
|---|
| Закончено |
У маленькой Рози на телефоне есть рабочий стол (или лаунчер, как его еще называют). Рабочий стол может состоять из нескольких экранов. Каждый экран представлен в виде сетки размером $$$5 \times 3$$$, то есть пять строк и три столбца.
Есть $$$x$$$ приложений с иконкой размером $$$1 \times 1$$$ ячеек, такая иконка занимает всего одну ячейку экрана. Также есть $$$y$$$ приложений с иконкой размером $$$2 \times 2$$$ ячейки, такая иконка занимает на экране квадрат из $$$4$$$ ячеек. Каждая ячейка каждого экрана может быть занята не более чем одной иконкой.
Рози хочет расположить иконки приложений на минимальном количестве экранов. Помогите ей найти такое количество экранов.
Первая строка ввода содержит $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных.
Первая и единственная строка каждого набора содержит два целых числа $$$x$$$ и $$$y$$$ ($$$0 \leq x, y \leq 99$$$) — количество приложений с иконкой $$$1 \times 1$$$ и количество приложений с иконкой $$$2 \times 2$$$ соответственно.
Для каждого набора входных данных выведите минимальное количество необходимых экранов на отдельной строке.
111 17 212 40 31 08 10 02 015 08 20 9
1 1 2 2 1 1 0 1 1 2 5
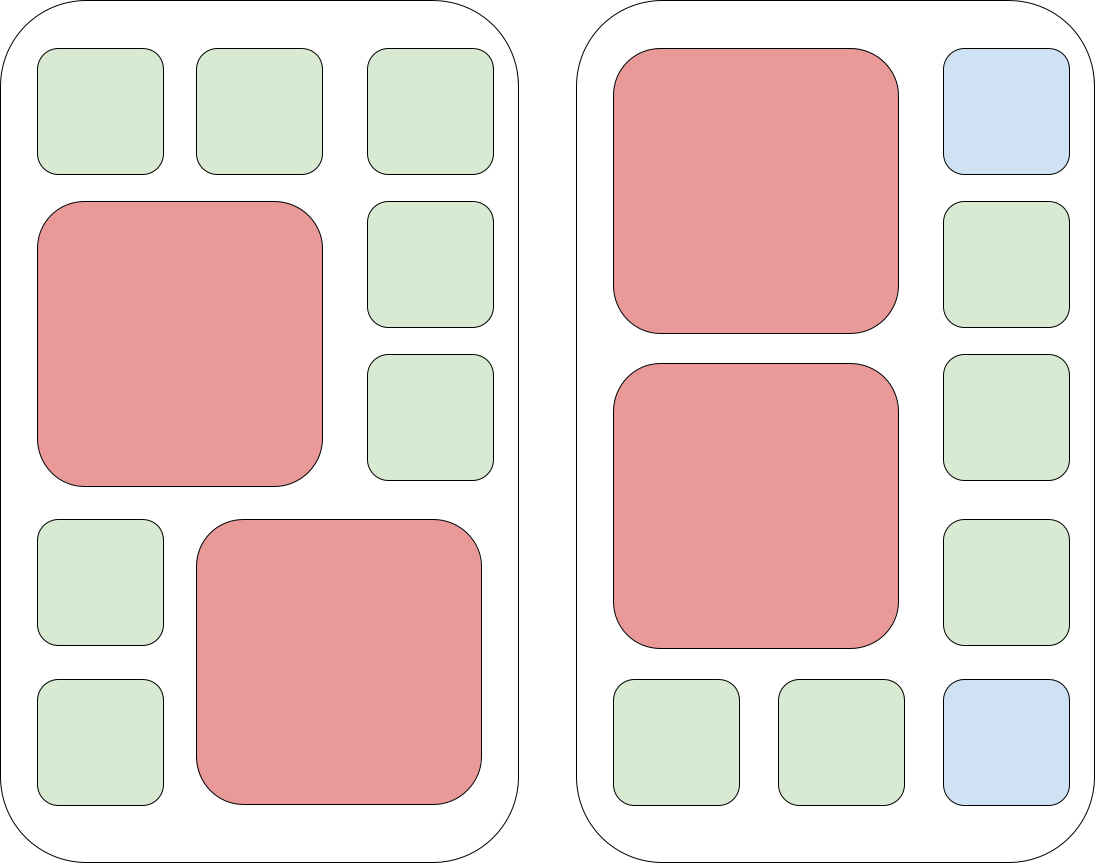
Решение для первого примера может выглядеть следующим образом:
 Синие квадраты представляют пустые места для иконок, зеленые квадраты представляют иконки $$$1 \times 1$$$, красные квадраты представляют иконки $$$2 \times 2$$$
Синие квадраты представляют пустые места для иконок, зеленые квадраты представляют иконки $$$1 \times 1$$$, красные квадраты представляют иконки $$$2 \times 2$$$ Решение для третьего примера может выглядеть следующим образом:
| Название |
|---|




