C. Как ходит ладья?
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Вам дана шахматная доска размером $$$n \times n$$$, на которой вы и компьютер поочередно расставляете белые и черные ладьи соответственно. Расставляя ладьи, вы должны следить за тем, чтобы никакие две ладьи не атаковали друг друга. Две ладьи атакуют друг друга, если они находятся в одной строке или столбце независимо от цвета.

Правильный ход — установка ладьи на позиции ($$$r$$$, $$$c$$$) так, чтобы она не атаковала никакую другую ладью.

Вы начинаете первым, и когда вы в свой ход сделаете правильный ход, поставив белую ладью на позицию ($$$r$$$, $$$c$$$), компьютер отзеркалит ваш ход и в свой ход поставит черную ладью на позицию ($$$c$$$, $$$r$$$). Если $$$r = c$$$, то компьютер не сможет отзеркалить ваш ход и пропустит его.

Вы уже сыграли с компьютером $$$k$$$ ходов (компьютер отразил и эти ходы), и вы должны продолжать игру, пока не останется ни одного правильного хода. Сколько различных конечных конфигураций можно получить, если продолжить игру после данных $$$k$$$ ходов? Гарантируется, что $$$k$$$ сделанных ходов были правильными. Так как ответ может быть большим, выведите его по модулю $$$10^9+7$$$.

Две конфигурации считаются различными, если существует координата ($$$r$$$, $$$c$$$), в которой ладья есть в одной конфигурации, но нет в другой, или цвет ладьи на координате отличается.

Входные данные

Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.

Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \leq n \leq 3 \cdot 10^5$$$, $$$0 \leq k \leq n$$$) — размер шахматной доски и количество ходов, которое вы уже сыграли соответственно.

Каждая из следующих $$$k$$$ строк набора входных данных содержит по два целых числа $$$r_i$$$ и $$$c_i$$$, описывающих ваш $$$i$$$-й ход.

Гарантируется, что все $$$k$$$ ходов являются правильными.

Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.

Выходные данные

Для каждого набора входных данных выведите в отдельной строке одно число — общее количество возможных конечных конфигураций по модулю $$$10^9+7$$$.

Пример
Входные данные
3
4 1
1 2
8 1
7 6
1000 4
4 4
952 343
222 333
90 91
Выходные данные
3
331
671968183
Примечание

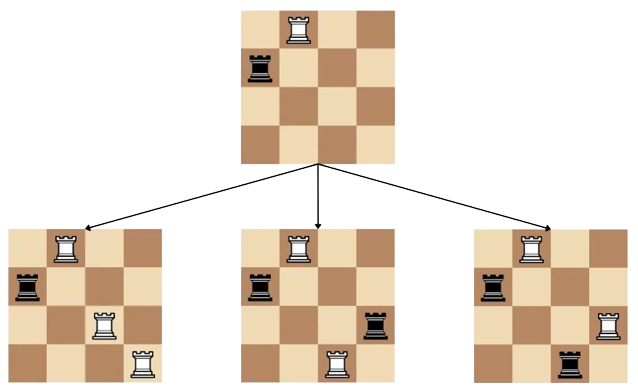
В первом наборе входных данных у нас есть поле $$$4 \times 4$$$, и вы уже сыграли $$$1$$$ ход. После того как вы и компьютер сыграли по одному ходу, на поле есть белая ладья на ($$$1$$$, $$$2$$$) и черная ладья на ($$$2$$$, $$$1$$$). Из этого состояния возможны три конфигурации —

  1. Вы ставите белую ладью на ($$$3$$$, $$$4$$$), а компьютер в ответ ставит черную ладью на ($$$4$$$, $$$3$$$).
  2. Вы ставите белую ладью на ($$$4$$$, $$$3$$$), а компьютер в ответ ставит черную ладью на ($$$3$$$, $$$4$$$).
  3. Вы ставите белую ладью на ($$$3$$$, $$$3$$$), а затем на ($$$4$$$, $$$4$$$), или наоборот. Оба варианта приводят к одной и той же конфигурации.