| Codeforces Round 935 (Div. 3) |
|---|
| Закончено |
В деревне Летово есть $$$n$$$ домов. Жители деревни решили построить большую дорогу, которая разделит деревню на левую и правую стороны. Житель каждого дома хочет жить либо на правой, либо на левой стороне улицы. Можно описать предпочтения в виде последовательности $$$a_1, a_2, \dots, a_n$$$, где $$$a_j = 0$$$, если житель $$$j$$$-го дома хочет жить на левой стороне улицы, иначе $$$a_j = 1$$$.
Дорога будет проходить между двумя домами, и дома слева от нее будут левыми, дома справа — правыми. Более формально, пусть дорога проходит между домами $$$i$$$ и $$$i+1$$$. Тогда дома на позициях от $$$1$$$ до $$$i$$$ будут на левой стороне улицы, а на позициях $$$i+1$$$ до $$$n$$$ на правой стороне. Дорога также может проходить перед первым или после последнего дома, в таком случае вся деревня объявляется правой или левой стороной соответственно.
Чтобы всё было честно, было решено спроектировать дорогу так, чтобы не менее половины жителей каждой из сторон деревни в отдельности остались довольны выбором. То есть среди $$$x$$$ жителей одной стороны, хотя бы $$$\lceil\frac{x}{2}\rceil$$$ должны хотеть жить именно на этой стороне, где $$$\lceil x \rceil$$$ означает округление вверх вещественного числа $$$x$$$.
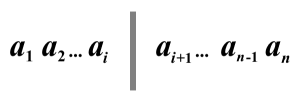 Слева от дороги будет $$$i$$$ домов, среди соответствующих $$$a_j$$$ должно быть не меньше $$$\lceil\frac{i}{2}\rceil$$$ нулей. Справа от дороги будет $$$n-i$$$ домов, среди соответствующих $$$a_j$$$ должно быть не меньше $$$\lceil\frac{n-i}{2}\rceil$$$ единиц.
Слева от дороги будет $$$i$$$ домов, среди соответствующих $$$a_j$$$ должно быть не меньше $$$\lceil\frac{i}{2}\rceil$$$ нулей. Справа от дороги будет $$$n-i$$$ домов, среди соответствующих $$$a_j$$$ должно быть не меньше $$$\lceil\frac{n-i}{2}\rceil$$$ единиц. Определите, после какого дома $$$i$$$ стоит проложить дорогу, чтобы выполнялось описанное условие и она была как можно ближе к середине деревни. Формально, среди всех подходящих позиций $$$i$$$ минимизируйте $$$\left|\frac{n}{2} - i\right|$$$.
Если подходящих позиций $$$i$$$ с минимальным $$$\left|\frac{n}{2} - i\right|$$$ несколько, выведите меньшую из них.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 2\cdot 10^4$$$) — количество наборов входных данных. Далее следуют описания наборов входных данных.
Первая строка каждого набора входных данных содержит одно число $$$n$$$ ($$$3 \le n \le 3\cdot 10^5$$$) — количество домов.
Следующая строка входных данных состоит из строки $$$a$$$ из $$$n$$$ символов, каждый символ равен либо $$$0$$$, либо $$$1$$$.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$3\cdot 10^5$$$.
Для каждого набора входных данных, выведите одно число $$$i$$$ — позицию такого дома, после которого надо проложить дорогу (если ее надо проложить перед первым домом, выведите $$$0$$$). Можно показать, что ответ всегда существует.
731016010111601100130003110300141100
2 3 2 3 0 1 0
Рассмотрим первый пример входных данных.
Если проложить дорогу после первого дома, на левой стороне улицы будет расположен один дом $$$a_1 = 1$$$, житель которого хотел бы жить на правой стороне улицы. Тогда $$$0$$$ из $$$1$$$ жителей левой стороны останутся довольны выбором, значит, после дома $$$1$$$ дорогу проложить нельзя.
Если проложить дорогу после второго дома, $$$1$$$ из $$$2$$$ жителей левой стороны (с пожеланиями $$$a_1 = 1$$$, $$$a_2 = 0$$$) и $$$1$$$ из $$$1$$$ жителя правой стороны (с пожеланием $$$a_3 = 1$$$) останутся довольны выбором. Более половины жителей каждой стороны довольны выбором, значит, после дома $$$2$$$ дорогу проложить разрешено. Можно показать, что это оптимальный ответ.
| Название |
|---|




