| Codeforces Round 933 (Div. 3) |
|---|
| Закончено |
Бернард любит ездить к Рудольфу в гости, но постоянно опаздывает. Проблема в том, что Бернард вынужден переплывать реку на пароме. Рудольф решил помочь своему другу решить эту проблему.
Река представляет собой клетчатое поле из $$$n$$$ строк и $$$m$$$ столбцов. На пересечении $$$i$$$-й строки и $$$j$$$-го столбца записано число $$$a_{i,j}$$$ — глубина в соответствующей клетке. Все клетки первого и последнего столбцов соответствуют берегам реки, поэтому глубина в них $$$0$$$.
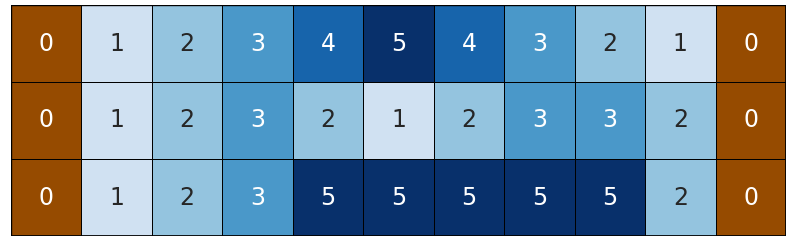 Река может выглядеть так.
Река может выглядеть так. Рудольф может выбрать строку $$$(i,1), (i,2), \ldots, (i,m)$$$ и построить над ней мост. В каждой клетке строки он может установить опору для моста. Стоимость установки опоры в клетке $$$(i,j)$$$ равна $$$a_{i,j}+1$$$. Опоры необходимо установить так, чтобы были выполнены следующие условия:
- В клетке $$$(i,1)$$$ должна быть установлена опора;
- В клетке $$$(i,m)$$$ должна быть установлена опора;
- Расстояние между любой парой соседних опор должно быть не больше $$$d$$$. Расстояние между опорами $$$(i, j_1)$$$ и $$$(i, j_2)$$$ равно $$$|j_1 - j_2| - 1$$$.
Построить один мост это скучно. Поэтому Рудольф решил построить $$$k$$$ мостов на последовательных строках реки, то есть выбрать некоторое $$$i$$$ ($$$1 \le i \le n - k + 1$$$) и независимо построить по мосту на каждой из строк $$$i, i + 1, \ldots, i + k - 1$$$. Помогите Рудольфу минимизировать суммарную стоимость установки опор.
Первая строка содержит одно целое число $$$t$$$ $$$(1 \le t \le 10^3)$$$ — количество наборов входных данных. Далее следуют описания наборов.
Первая строка каждого набора данных содержит четыре целых числа $$$n$$$, $$$m$$$, $$$k$$$ и $$$d$$$ ($$$1 \le k \le n \le 100$$$, $$$3 \le m \le 2 \cdot 10^5$$$, $$$1 \le d \le m$$$) — количество строк и столбцов поля, количество мостов, максимальное расстояние между опорами.
Далее следует $$$n$$$ строк, $$$i$$$-я строка содержит $$$m$$$ целых положительных чисел $$$a_{i, j}$$$ ($$$0 \le a_{i, j} \le 10^6$$$, $$$a_{i, 1} = a_{i, m} = 0$$$) — глубины клеток реки.
Гарантируется, что сумма $$$n \cdot m$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно число — минимальную суммарную стоимость опор.
53 11 1 40 1 2 3 4 5 4 3 2 1 00 1 2 3 2 1 2 3 3 2 00 1 2 3 5 5 5 5 5 2 04 4 2 10 3 3 00 2 1 00 1 2 00 3 3 04 5 2 50 1 1 1 00 2 2 2 00 2 1 1 00 3 2 1 01 8 1 10 10 4 8 4 4 2 04 5 3 20 8 4 4 00 3 4 8 00 8 1 10 00 10 1 5 0
4 8 4 15 14
В первом наборе тестовых данных выгоднее всего построить мост на второй строке.
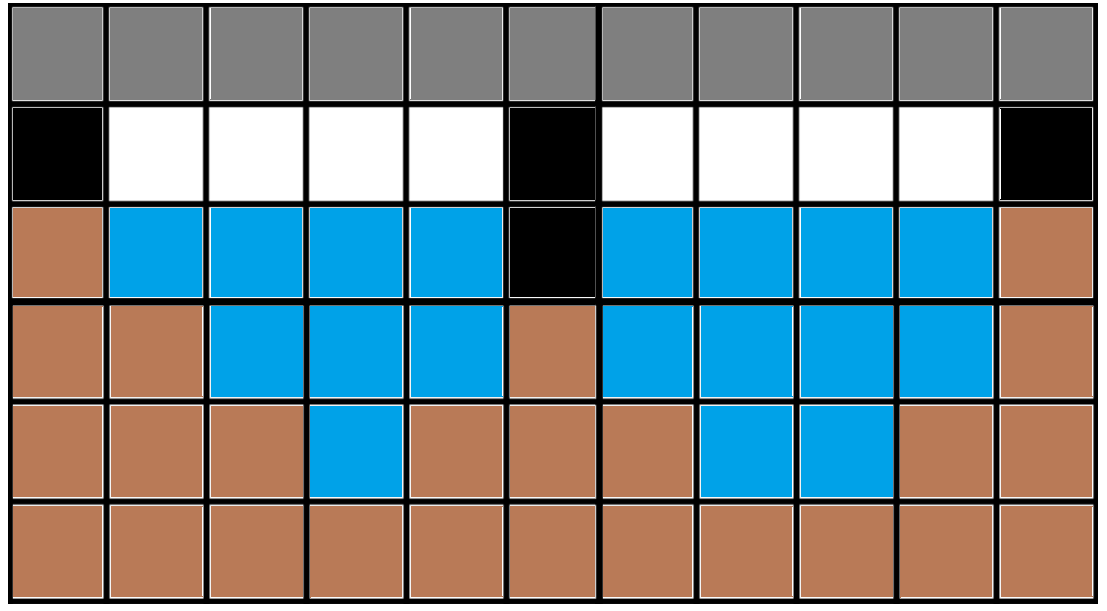 Это не вид сверху, а вид сбоку: серые ячейки — сам мост, белые ячейки — пустые, черные ячейки — опоры, синие ячейки — вода, коричневые ячейки — дно реки.
Это не вид сверху, а вид сбоку: серые ячейки — сам мост, белые ячейки — пустые, черные ячейки — опоры, синие ячейки — вода, коричневые ячейки — дно реки. Во втором наборе мост выгоднее всего построить на второй и третьей строках. Опоры будут стоять в клетках $$$(2, 3)$$$, $$$(3, 2)$$$ и на берегах.
В третьем наборе опоры можно расположить по берегам.
| Название |
|---|




