| Codeforces Round 932 (Div. 2) |
|---|
| Закончено |
Магистр Андрей очень любит деревья$$$^{\dagger}$$$, поэтому у него есть дерево, состоящее из $$$n$$$ вершин.
Но не все так просто. Магистр Тимофей решил украсть одну вершину из дерева. Если Тимофей украл вершину $$$v$$$ из дерева, то вершина $$$v$$$ и все ребра с концом в вершине $$$v$$$ удаляются из дерева, при этом номера других вершин не меняются. Чтобы Андрей не расстраивался, Тимофей решил сделать получившийся граф снова деревом. Для этого он может добавлять ребра между произвольными вершинами $$$a$$$ и $$$b$$$, однако при добавлении такого ребра он должен заплатить $$$|a - b|$$$ монет в Центр Помощи Магистрам.
Обратите внимание, что получившееся дерево не содержит вершину $$$v$$$.
Тимофей не определился, какую вершину $$$v$$$ он удалит из дерева, поэтому он хочет знать для каждой вершины $$$1 \leq v \leq n$$$, какое минимальное количество монет нужно потратить, чтобы после удаления вершины $$$v$$$ сделать граф снова деревом, а также какие ребра при этом нужно добавить.
$$$^{\dagger}$$$Деревом называется неориентированный связный граф без циклов.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$5 \le n \le 2\cdot10^5$$$) — количество вершин в дереве Андрея.
В следующих $$$n - 1$$$ строках содержится описание ребер дерева. $$$i$$$-я из этих строк содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$) — номера вершин, соединённых $$$i$$$-м ребром.
Гарантируется, что данные рёбра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2\cdot10^5$$$.
Для каждого набора входных данных выведите ответ в следующем формате:
Для каждой вершины $$$v$$$ (в порядке от $$$1$$$ до $$$n$$$) в первой строке выведите два целых числа $$$w$$$ и $$$m$$$ — минимальное количество монет, которое нужно потратить, чтобы граф после удаления вершины $$$v$$$ снова стал деревом, и количество добавленных ребер.
Далее выведите $$$m$$$ строк, каждая из которых содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n, a \ne v, b \ne v$$$, $$$a \ne b$$$) — концы добавленного ребра.
Если существует несколько способов добавить ребра, вы можете вывести любое решение с минимальной стоимостью.
351 31 44 53 254 24 33 55 152 11 51 41 3
1 1 3 4 0 0 1 1 1 2 2 1 3 5 0 0 0 0 0 0 1 1 1 2 1 1 1 2 1 1 1 2 3 3 2 3 4 5 3 4 0 0 0 0 0 0 0 0
В первом наборе входных данных:
Рассмотрим удаление вершины $$$4$$$:
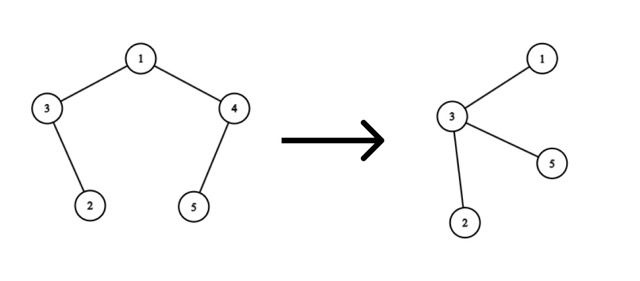
Оптимальным решением будет провести ребро из вершины $$$5$$$ в вершину $$$3$$$. Тогда мы потратим $$$|5 - 3| = 2$$$ монеты.
В третьем наборе входных данных:
Рассмотрим удаление вершины $$$1$$$:
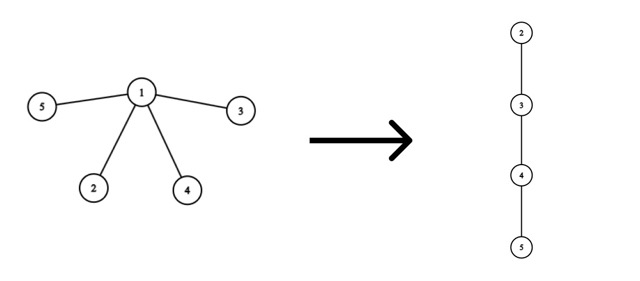
Оптимальным решением будет:
- Провести ребро из вершины $$$2$$$ в вершину $$$3$$$, потратив $$$|2 - 3| = 1$$$ монету.
- Провести ребро из вершины $$$3$$$ в вершину $$$4$$$, потратив $$$|3 - 4| = 1$$$ монету.
- Провести ребро из вершины $$$4$$$ в вершину $$$5$$$, потратив $$$|4 - 5| = 1$$$ монету.
Тогда сумарно мы потратим $$$1 + 1 + 1 = 3$$$ монеты.
Рассмотрим удаление вершины $$$2$$$:
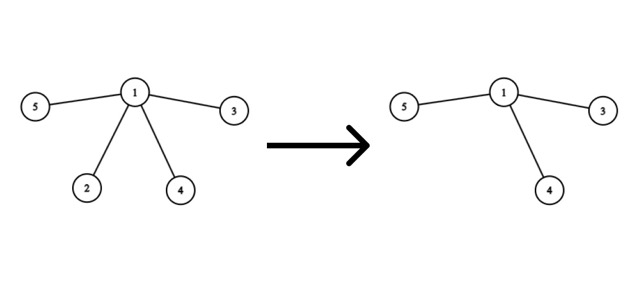
Ребра проводить не нужно, так как после удаления вершины граф останется деревом.
| Название |
|---|




