| Codeforces Round 122 (Div. 1) |
|---|
| Закончено |
Дан лист клетчатой бумаги n × m. Некоторые его клетки закрашены. Множество всех закрашенных клеток листа бумаги обозначим через A. Множество A является связным. Требуется найти минимальное количество клеток, которые можно удалить из множества A так, чтобы оно перестало быть связным.
Множество закрашенных клеток называется связным, если для каждых двух клеток из этого множества a и b найдется последовательность клеток множества, начинающаяся в a и заканчивающаяся в b, такая, что любая клетка этой последовательности, исключая последнюю, имеет общую сторону со следующей в последовательности клеткой. Пустое множество и множество, состоящее из одной клетки, по определению считаются связными.
В первой строке входного файла записаны через пробел два целых числа n и m (1 ≤ n, m ≤ 50) — размеры листа бумаги.
В следующих n строках содержится по m символов — описание листа бумаги: j-й символ i-й строки равен «#», если соответствующая клетка закрашена (принадлежит множеству A), или равен «.», если соответствующая клетка не закрашена (не принадлежит множеству A). Гарантируется, что множество всех закрашенных клеток A связно и не пусто.
На первой строке выведите минимальное количество клеток, которые нужно удалить, чтобы лишить множество A связности или -1, если это невозможно.
5 4
####
#..#
#..#
#..#
####
2
5 5
#####
#...#
#####
#...#
#####
2
В первом примере можно удалить любые две клетки, не имеющие общей стороны и множество закрашенных клеток потеряет связность.
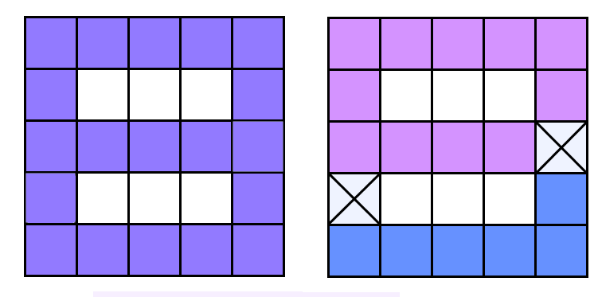
Пояснение ко второму примеру изображено на рисунке. Слева изображено изначальное множество клеток. Справа — множество с удаленными клетками. Удаленные клетки помечены крестиками.
| Название |
|---|




