| Codeforces Round 926 (Div. 2) |
|---|
| Закончено |
Саше за победу на очередной олимпиаде подарили дерево$$$^{\dagger}$$$ из $$$n$$$ вершин. Но, вернувшись домой после празднования очередной победы, он заметил его потерю. Саша помнит, что он покрасил некоторые рёбра этого дерева. При этом он точно знает, что для любой из $$$k$$$ пар вершин $$$(a_1, b_1), \ldots, (a_k, b_k)$$$ он покрасил хотя бы одно ребро на простом пути$$$^{\ddagger}$$$ между вершинами $$$a_i$$$ и $$$b_i$$$.
Саша не помнит, сколько рёбер он точно покрасил, так что он просит вас сказать, какое минимальное количество рёбер он мог покрасить, чтобы выполнялось описанное выше условие.
$$$^{\dagger}$$$Деревом называется неориентированный связный граф без циклов.
$$$^{\ddagger}$$$Простой путь — это путь, проходящий через каждую вершину не более одного раза.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 10^5$$$) — количество вершин в дереве.
Следующие $$$(n - 1)$$$ строка описывают рёбра дерева. $$$i$$$-я из них содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \ne v_i$$$) — номера вершин, которые соединяет $$$i$$$-е ребро.
Следующая строка содержит одно целое число $$$k$$$ ($$$1 \leq k \leq 20$$$) — количество пар вершин, на простом пути между которыми Саша покрасил хотя бы одно ребро.
Следующие $$$k$$$ строк описывают пары. $$$j$$$-я из них содержит два целых числа $$$a_j$$$ и $$$b_j$$$ ($$$1 \leq a_j, b_j \leq n, a_j \neq b_j$$$) — вершины в $$$j$$$-й паре.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$. Гарантируется, что сумма $$$2^k$$$ по всем наборам входных данных не превосходит $$$2^{20}$$$.
Для каждого набора входных данных выведите одно целое число — минимальное количество рёбер, которое мог покрасить Саша.
341 22 32 421 34 161 23 16 15 24 233 13 62 651 22 33 44 541 22 33 44 5
1 2 4
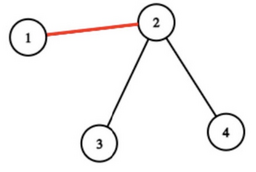
В первом наборе входных данных Саша мог покрасить только одно ребро $$$(1, 2)$$$. Тогда на простом пути между вершинами $$$1$$$ и $$$3$$$ и вершинами $$$4$$$ и $$$1$$$ будет хотя бы одно покрашенное ребро.
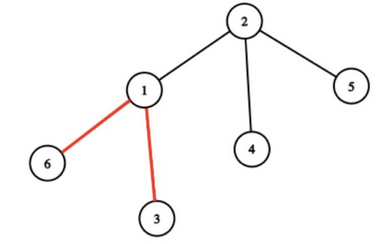
Во втором наборе входных данных Саша мог покрасить рёбра $$$(1, 6)$$$ и $$$(1, 3)$$$.
| Название |
|---|




