| Codeforces Round 926 (Div. 2) |
|---|
| Закончено |
Саша хочет прогуляться со своей девушкой по городу. Город состоит из $$$n$$$ перекрёстков, пронумерованных от $$$1$$$ до $$$n$$$. Некоторые из них соединены дорогами, причём от любого перекрёстка существует ровно один простой путь$$$^{\dagger}$$$ до любого другого перекрёстка. Другими словами, перекрёстки и дороги между ними образуют дерево.
Некоторые из перекрёстков являются опасными. И так как гулять одним по городу небезопасно, то Саша не хочет за время прогулки посещать три и более опасных перекрёстков.
Саша называет множество перекрёстков хорошим, если выполняется следующее условие:
- Если в городе опасными являются те и только те перекрёстки, которые содержатся в этом множестве, то любой простой путь в городе содержит не более двух опасных перекрёстков.
Однако Саша не знает, какие из перекрёстков являются опасными, поэтому его интересует количество различных хороших множеств перекрёстков, которые есть в городе. Поскольку это количество может быть очень большим, выведите его по модулю $$$998\,244\,353$$$.
$$$^{\dagger}$$$Простой путь — это путь, проходящий через каждый перекрёсток не более одного раза.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \leq 3 \cdot 10^5$$$) — количество перекрёстков в городе.
Следующие $$$(n - 1)$$$ строка описывают дороги. $$$i$$$-я из них содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \ne v_i$$$) — номера перекрёстков, которые соединяет $$$i$$$-я дорога.
Гарантируется, что данные дороги образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — количество хороших множеств перекрёстков по модулю $$$998\,244\,353$$$.
431 33 243 42 33 151 23 45 12 341 22 33 4
7 12 16 11
В первом наборе входных данных всего есть $$$2^3 = 8$$$ множеств перекрёстков. Все из них являются хорошими, кроме множества $$$\{1, 2, 3\}$$$, потому что, если перекрёстки $$$1, 2$$$ и $$$3$$$ являются опасными, то простой путь $$$1 - 2 - 3$$$ содержит $$$3$$$ опасных перекрёстка. Таким образом, всего есть $$$7$$$ хороших множеств.
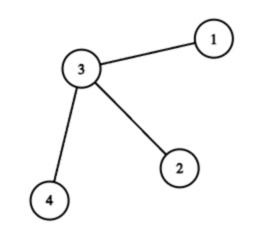
Во втором наборе входных данных всего есть $$$2^4 = 16$$$ множеств перекрёстков. При этом множества $$$\{1, 2, 3, 4\}$$$, $$$\{1, 2, 3\}$$$, $$$\{1, 3, 4\}$$$, $$$\{2, 3, 4\}$$$ не являются хорошими. Таким образом, всего есть $$$12$$$ хороших множеств. Ниже изображена схема города:
| Название |
|---|




