| Codeforces Round 924 (Div. 2) |
|---|
| Закончено |
У Боба есть прямоугольник размера $$$a \times b$$$. Он пробует разрезать этот прямоугольник на два прямоугольника с целыми сторонами, сделав разрез, параллельный какой-то из сторон исходного прямоугольника. Затем Боб пытается из двух получившихся прямоугольников сложить какой-то другой прямоугольник, при этом он может как угодно поворачивать и двигать эти два прямоугольника.
Обратите внимание, что если два прямоугольника отличаются поворотом на $$$90^{\circ}$$$, то они считаются одинаковыми. Например, прямоугольники $$$6 \times 4$$$ и $$$4 \times 6$$$ считаются одинаковыми.
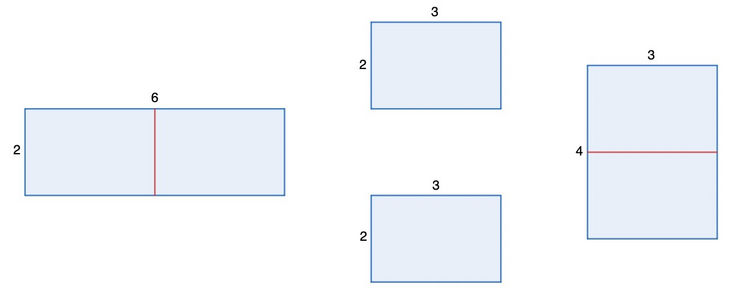
Таким образом, из прямоугольника $$$2 \times 6$$$ можно получить другой прямоугольник, потому что его можно разрезать на два прямоугольника $$$2 \times 3$$$, после чего из этих двух прямоугольников сложить прямоугольник $$$4 \times 3$$$, который отличается от прямоугольника $$$2 \times 6$$$.
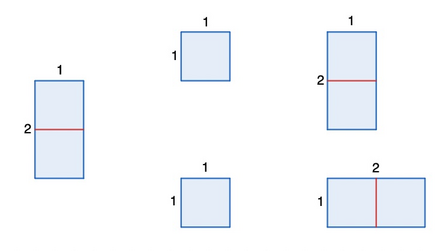
При этом из прямоугольника $$$2 \times 1$$$ нельзя получить другой прямоугольник, потому что его можно разрезать только на два прямоугольника $$$1 \times 1$$$, а из них можно сложить только прямоугольники $$$1 \times 2$$$ и $$$2 \times 1$$$, которые считаются одинаковыми.
Помогите Бобу определить, сможет ли он получить какой-то другой прямоугольник, или он только зря тратит время.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Единственная строка каждого набора входных данных содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le 10^9$$$) — размеры прямоугольника Боба.
Для каждого набора входных данных выведите «Yes», если Боб может получить другой прямоугольник из прямоугольника $$$a \times b$$$. Иначе выведите «No».
Вы можете вывести ответ в любом регистре (верхнем или нижнем). Например, строки «yEs»,«yes», «Yes» и «YES» будут распознаны как положительные ответы.
71 12 12 63 22 22 46 3
No No Yes Yes Yes Yes No
В первом наборе входных данных прямоугольник $$$1 \times 1$$$ нельзя разрезать на два прямоугольника, поэтому из него нельзя получить другой прямоугольник.
Во четвёртом наборе входных данных прямоугольник $$$3 \times 2$$$ можно разрезать на два прямоугольника $$$3 \times 1$$$, а из них можно сложить прямоугольник $$$1 \times 6$$$.
В пятом наборе входных данных прямоугольник $$$2 \times 2$$$ можно разрезать на два прямоугольника $$$1 \times 2$$$, а из них можно сложить прямоугольник $$$1 \times 4$$$.
| Название |
|---|




