G. Влад и проблемы в МИТ
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

У Владислава есть сын, который очень хотел поступить в МИТ. Общежитие колледжа в МИТ (Молдавский институт технологий) можно представить в виде дерева с $$$n$$$ вершинами, где каждая вершина представляет собой комнату с ровно одним студентом. Дерево — это связный неориентированный граф с $$$n$$$ вершинами и $$$n-1$$$ ребром.

Сегодня ночью есть три типа студентов:

  • студенты, которые хотят веселиться и слушать музыку (обозначены $$$\texttt{P}$$$),
  • студенты, которые хотят спать и наслаждаться тишиной (обозначены $$$\texttt{S}$$$), и
  • студенты, которым не важно, что делать ночью (обозначены $$$\texttt{C}$$$).

Изначально все рёбра представляют собой тонкие стены, которые позволяют музыке проходить через них, поэтому когда веселящийся студент включает музыку, её можно услышать в каждой комнате. Однако мы можем установить толстые стены на любые рёбра — толстые стены не позволяют музыке проходить через них.

Университет хочет установить несколько толстых стен, чтобы каждый веселящийся студент мог слушать музыку, и ни один спящий студент не мог её услышать.

Поскольку университет потерял много денег в судебном процессе о правах на наименование, они просят вас найти минимальное количество толстых стен, которые им придется использовать.

Входные данные

Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных.

Первая строка каждого набора содержит целое число $$$n$$$ ($$$2 \leq n \leq 10^5$$$) — количество вершин в дереве.

Вторая строка каждого набора входных данных содержит $$$n-1$$$ целых чисел $$$a_2, \dots , a_n$$$ ($$$1 \leq a_i < i$$$) — это означает, что есть ребро между $$$i$$$ и $$$a_i$$$ в дереве.

Третья строка каждого набора входных данных содержит строку $$$s$$$ длиной $$$n$$$, состоящую из символов $$$\texttt{P}$$$, $$$\texttt{S}$$$ и $$$\texttt{C}$$$, обозначающих, что студент $$$i$$$ относится к типу $$$s_i$$$.

Сумма $$$n$$$ по всем наборам входных данных не превышает $$$10^5$$$.

Выходные данные

Для каждого набора входных данных выведите одно целое число — искомое минимальное количество толстых стен.

Пример
Входные данные
3
3
1 1
CSP
4
1 2 2
PCSS
4
1 2 2
PPSS
Выходные данные
1
1
2
Примечание

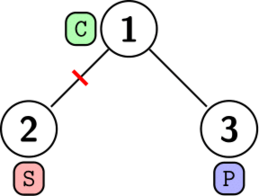
В первом случае мы можем установить одну толстую стену между комнатами $$$1$$$ и $$$2$$$, как показано ниже. Мы не можем установить $$$0$$$ стен, так как тогда музыка из комнаты 3 дойдет до комнаты 2, где студент хочет спать, поэтому ответ равен $$$1$$$. Существуют и другие допустимые решения.