| Hello 2024 |
|---|
| Закончено |
Есть ребро-взвешенное полное двоичное дерево с $$$n$$$ листьями. Полное двоичное дерево определяется как дерево, в котором каждая нелистовая вершина имеет ровно 2 дочерних вершины. Для каждой нелистовой вершины обозначим одного из ее детей как левого ребенка, а другого — как правого.
Это двоичное дерево обладает очень странным свойством. Для каждой нелистовой вершины одно из ребер к ее детям имеет вес $$$0$$$, а другое ребро — вес $$$1$$$. Обратите внимание, что ребро с весом $$$0$$$ может идти как к левому ребенку, так и к правому.
Вы забыли, как выглядит дерево, но, к счастью, вы помните некоторую информацию о листьях в виде массива $$$a$$$ длины $$$n$$$. Для каждого $$$i$$$ от $$$1$$$ до $$$n$$$, $$$a_i$$$ представляет собой расстояние$$$^\dagger$$$ от корня до $$$i$$$-го листа (в порядке обхода dfs$$$^\ddagger$$$). Определите, существует ли полное двоичное дерево, удовлетворяющее массиву $$$a$$$. Обратите внимание, что восстанавливать дерево не нужно.
$$$^\dagger$$$ Расстояние от вершины $$$u$$$ до вершины $$$v$$$ определяется как сумма весов ребер на пути от вершины $$$u$$$ до вершины $$$v$$$.
$$$^\ddagger$$$ Порядок листьев в dfs определяется вызовом следующей функции $$$\texttt{dfs}$$$ на корне бинарного дерева.
dfs_order = [] — порядок обхода dfs
функция dfs(v):
если v — лист:
добавить v в конец dfs_order
иначе:
dfs(левый ребенок v)
dfs(правый ребенок v)
dfs(корень)
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 2\cdot 10^5$$$) — длину массива $$$a$$$.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \le a_i \le n - 1$$$) — расстояние от корня до $$$i$$$-го листа.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите «YES», если существует полное двоичное дерево, удовлетворяющее массиву $$$a$$$, и «NO» в противном случае.
Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ.
252 1 0 1 151 0 2 1 3
YES NO
В первом наборе входных данных массиву удовлетворяет следующее дерево.
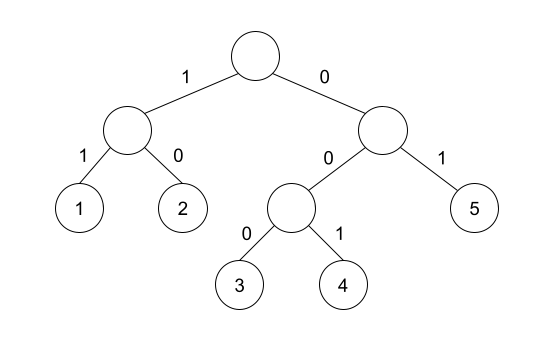
Для второго набора входных данных можно доказать, что не существует полного двоичного дерева, удовлетворяющего массиву.
| Название |
|---|




