| 2023-2024 ICPC, NERC, Northern Eurasia Onsite (Unrated, Online Mirror, ICPC Rules, Teams Preferred) |
|---|
| Закончено |
The city of F. can be represented as a tree. A famous fugitive is hiding in it, and today a faithful police officer decided to catch him at all costs. The police officer is stronger than the fugitive, but the fugitive is much faster than the former. That is why the pursuit proceeds as follows. At the moment $$$t = 0$$$ the police officer appears at the vertex with number $$$s$$$, and the fugitive spawns at any other vertex of his choice. After that, they take turns, starting with the police officer.
- During the police officer's move, she selects any vertex adjacent to the one where she is currently located and moves there. The police officer spends one minute moving. Also, the police officer may decide to stand still instead, in which case she waits one minute at the vertex at which she started her move. If at the end of the turn the police officer ends up at the same vertex as the fugitive, she instantly catches him and the chase ends.
- The fugitive's move is as follows. Let him be at vertex $$$b$$$, and the police officer at vertex $$$p$$$. Then the fugitive chooses any vertex $$$b' \ne p$$$ such that the path between the vertices $$$b$$$ and $$$b'$$$ does not contain vertex $$$p$$$ and instantly moves there. In particular, he can always choose $$$b' = b$$$ to stay where he is. The fugitive's move takes no time.
Note that the fugitive managed to attach a radio bug to the police officer's badge a week ago, so the fugitive knows the location of the police officer at every moment (in particular, he knows the number $$$s$$$). On the contrary, the police officer knows nothing about the fugitive's movements and will only be able to detect him at the very moment she catches him.
The police officer aims to catch the fugitive as fast as possible, and the fugitive aims to be caught as late as possible. Since the chase can be thought of as a game with incomplete information, participants can use mixed (probabilistic) strategies — thus, the police officer acts to minimize the expected duration of the chase, and the fugitive — to maximize it.
Find the mathematical expectation of the duration of the chase with optimal actions of the police officer and the fugitive. It can be proven that it is always finite. In particular, with optimal strategies, the probability that the chase continues indefinitely is equal to zero.
The first line contains an integer $$$n$$$ — the number of vertices in the tree ($$$2 \le n \le 100$$$). The next $$$n - 1$$$ lines describe the city of F.: each of them contains a pair of integers $$$u_i$$$, $$$v_i$$$ — the numbers of the ends of an edge ($$$1 \le u_i, v_i \le n$$$). These edges are guaranteed to form a tree.
The last line contains an integer $$$s$$$ — the number of the vertex where the police officer initially appears ($$$1 \le s \le n$$$).
Print one real number — the mathematical expectation of the duration of the chase with the optimal strategies of the police officer and the fugitive. Your answer will be accepted if its absolute or relative error does not exceed $$$10^{-6}$$$; formally, if $$$p$$$ is your answer, and $$$j$$$ is the jury's answer, this should hold: $$$\frac{|p - j|}{\max\{1, |j|\}} \le 10^{-6}$$$.
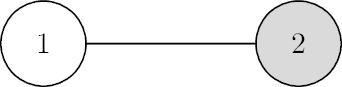
21 22
1
31 21 31
2
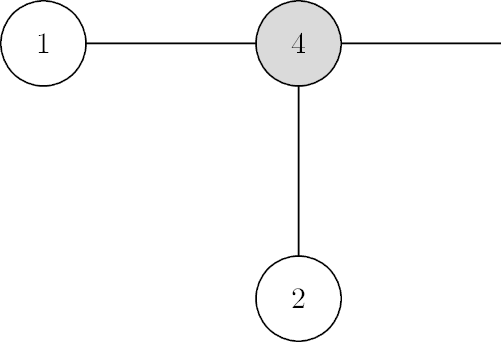
44 34 14 24
3.66667
71 44 55 24 66 77 33
8.3525
The trees from the examples are depicted below.


| Название |
|---|




