| Codeforces Round 915 (Div. 2) |
|---|
| Закончено |
В этом грустном мире, полном недостатков, существуют уродливые деревья отрезков.
Дерево отрезков — это дерево, где каждая вершина соответствует некоторому отрезку и имеет свой номер. Дерево отрезков для массива из $$$n$$$ элементов можно построить рекурсивно. Пусть функция $$$\operatorname{build}(v,l,r)$$$ строит дерево отрезков, корневая вершина которого имеет номер $$$v$$$ и соответствует отрезку $$$[l,r]$$$.
Теперь давайте определим $$$\operatorname{build}(v,l,r)$$$:
- Если $$$l=r$$$, то вершина $$$v$$$ является листом, поэтому мы прекращаем добавление новых рёбер;
- Иначе, мы добавляем рёбра $$$(v, 2v)$$$ и $$$(v, 2v+1)$$$. Пусть $$$m=\lfloor \frac{l+r}{2} \rfloor$$$. Затем мы вызываем $$$\operatorname{build}(2v,l,m)$$$ и $$$\operatorname{build}(2v+1,m+1,r)$$$.
Таким образом, всё дерево строится путём вызова $$$\operatorname{build}(1,1,n)$$$.
Теперь Ибти построит дерево отрезков для массива из $$$n$$$ элементов. Он хочет найти сумму всех $$$\operatorname{lca}^\dagger(S)$$$, где $$$S$$$ — непустое подмножество листьев. Обратите внимание, что существует ровно $$$2^n - 1$$$ возможных подмножеств. Поскольку эта сумма может быть очень большой, выведите её по модулю $$$998\,244\,353$$$.
$$$^\dagger\operatorname{lca}(S)$$$ — номер наименьшего общего предка для вершин, находящихся в $$$S$$$.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^3$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 10^{18}$$$) — длина массива, для которого строится дерево отрезков.
Для каждого набора входных данных выведите одно целое число — требуемую сумму по модулю $$$998\,244\,353$$$.
5234553278
6 17 36 69 593324855
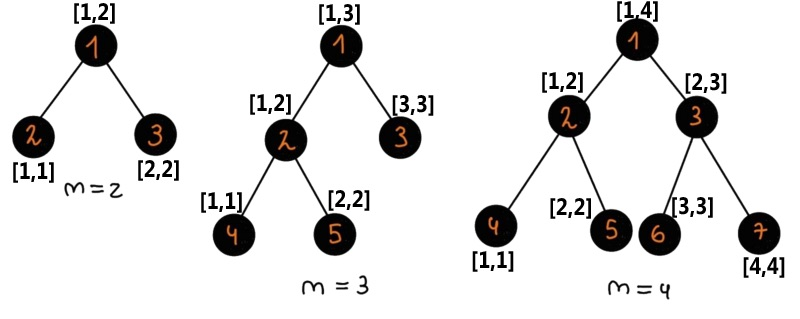
В первом наборе входных данных:
Давайте рассмотрим все подмножества листьев.
- $$$\operatorname{lca}(\{2\})=2$$$;
- $$$\operatorname{lca}(\{3\})=3$$$;
- $$$\operatorname{lca}(\{2,3\})=1$$$.
Таким образом, ответ равен $$$2+3+1=6$$$.
Во втором наборе входных данных:
Давайте рассмотрим все подмножества листьев.
- $$$\operatorname{lca}(\{4\})=4$$$;
- $$$\operatorname{lca}(\{5\})=5$$$;
- $$$\operatorname{lca}(\{3\})=3$$$;
- $$$\operatorname{lca}(\{4,5\})=2$$$;
- $$$\operatorname{lca}(\{4,3\})=1$$$;
- $$$\operatorname{lca}(\{5,3\})=1$$$;
- $$$\operatorname{lca}(\{4,5,3\})=1$$$;
Таким образом, ответ равен $$$4+5+3+2+1+1+1=17$$$.
| Название |
|---|




