| Codeforces Round 915 (Div. 2) |
|---|
| Закончено |
Вам дано дерево$$$^{\dagger}$$$. За одну зельда-операцию вы можете сделать следующее:
- Выбрать две вершины дерева $$$u$$$ и $$$v$$$;
- Сжать все вершины на пути от $$$u$$$ до $$$v$$$ в одну вершину. Другими словами, все вершины на пути от $$$u$$$ до $$$v$$$ будут удалены из дерева, будет создана новая вершина $$$w$$$. Затем каждая вершина $$$s$$$, которая имела ребро с какой-то вершиной на пути от $$$u$$$ до $$$v$$$, будет иметь ребро с вершиной $$$w$$$.
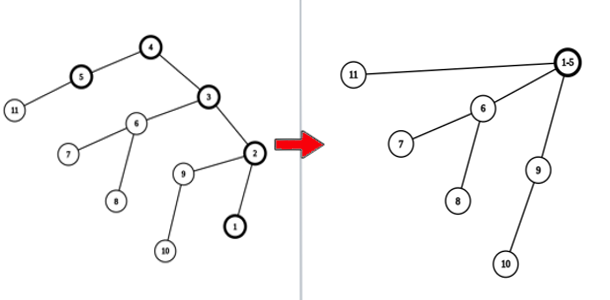 Иллюстрация результата зельда-операции для вершин $$$1$$$ и $$$5$$$.
Иллюстрация результата зельда-операции для вершин $$$1$$$ и $$$5$$$. Определите минимальное количество зельда-операций, необходимых для того, чтобы в дереве осталась только одна вершина.
$$$^{\dagger}$$$Дерево — это неориентированный связный граф без циклов.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество вершин.
$$$i$$$-я из следующих $$$n − 1$$$ строк содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n, u_i \ne v_i$$$) — номера вершин, соединенных $$$i$$$-м ребром.
Гарантируется, что заданные рёбра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$10^5$$$.
Для каждого набора входных данных выведите единственное целое число — минимальное количество зельда-операций, необходимых для того, чтобы в дереве осталась только одна вершина.
441 21 33 493 13 53 25 66 77 87 96 471 21 32 44 53 62 761 21 31 44 52 6
1 3 2 2
В первом наборе входных данных достаточно выполнить одну зельда-операцию для вершин $$$2$$$ и $$$4$$$.
Во втором наборе входных данных мы можем выполнить следующие зельда-операции:
- $$$u = 2, v = 1$$$. Пусть добавленная вершина будет обозначена как $$$w = 10$$$;
- $$$u = 4, v = 9$$$. Пусть добавленная вершина будет обозначена как $$$w = 11$$$;
- $$$u = 8, v = 10$$$. После этой операции дерево состоит из одной вершины.
| Название |
|---|




