| Codeforces Round 912 (Div. 2) |
|---|
| Закончено |
Теофанис хочет играть в видеоигры, но при этом он должен заботиться о своей сестре. Поскольку Теофанис учится на программиста, он нашел способ делать и то, и другое. Он установит в своем доме несколько камер, чтобы убедиться, что с его сестрой все в порядке.
Его дом — это неориентированный граф с $$$n$$$ вершинами и $$$m$$$ ребрами. Его сестра любит играть на ребрах графа, поэтому он должен установить камеру хотя бы в одном из концов каждого ребра графа. Теофанис хочет найти вершинное покрытие, которое максимизирует минимальную разницу между номерами выбранных вершин.
Более формально, пусть $$$a_1, a_2, \ldots, a_k$$$ — вершинное покрытие графа. Пусть минимальная разница между номерами выбранных вершин — это минимальное $$$\lvert a_i - a_j \rvert$$$ (где $$$i \neq j$$$) среди вершин, которые вы выбрали. Если $$$k = 1$$$, то считаем, что минимальная разница между номерами выбранных вершин равна $$$n$$$.
Можете ли вы найти максимально возможную минимальную разницу между номерами выбранных вершин?
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 10^{5}, 1 \le m \le 2 \cdot 10^{5}$$$) — количество вершин и количество ребер.
В $$$i$$$-й из следующих $$$m$$$ строк содержатся два целых положительных числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i,v_i \le n$$$), обозначающие, что между ними в графе существует ребро.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^{5}$$$.
Гарантируется, что сумма $$$m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^{5}$$$.
Для каждого набора входных данных выведите максимум среди минимальных разностей между выбранными вершинами среди всех вершинных покрытий.
37 61 21 31 41 62 35 73 31 21 31 12 41 21 22 11 1
2 3 2
В первом наборе входных данных мы можем установить камеры в вершинах $$$1$$$, $$$3$$$ и $$$7$$$, поэтому ответ — $$$2$$$.
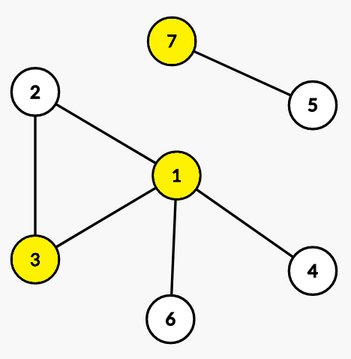
Во втором наборе входных данных мы можем установить только одну камеру в вершине $$$1$$$, поэтому ответ равен $$$3$$$.
| Название |
|---|




