Вас назначили на очень важное дело: подготовиться к выравниванию одной особой дороги.
Дорогу можно представить как ломаную линию, начинающуюся в $$$(0, 0)$$$ и заканчивающуюся в $$$(n - 1, 0)$$$, которая состоит из $$$n$$$ вершин (включая стартовую и финишную). Координаты $$$i$$$-й вершины ломаной равны $$$(i, a_i)$$$.
«Выравнивание» дороги эквивалентно выбору некоторого отрезка из $$$(0, y_0)$$$ в $$$(n - 1, y_1)$$$ такого, что все точки ломаной находятся ниже выбранного отрезка (или на той же высоте). Значения $$$y_0$$$ и $$$y_1$$$ могут быть действительными числами.
Вы можете представить, что первоначально на дороге есть всякие ямы и ухабы, и вы начинаете насыпать на нее покрытие, пока не сделаете ее ровной. Для простоты, в точках $$$0$$$ и $$$n - 1$$$ находятся бесконечно высокие стены, а потому покрытие не вываливается наружу отрезка $$$[0, n - 1]$$$.
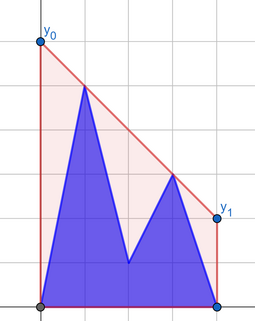
Цена выровненной дороги равна площади между выбранным отрезком и ломаной. Вы хотите минимизировать эту цену, а потому выровненная дорога будет необязательно горизонтальной.
Но есть одна проблема: ваша информация могла устареть. А потому вы отправили специального человека померить новые высоты. Этот человек идет из $$$0$$$ в $$$n - 1$$$ и посылает вам новые высоты $$$b_i$$$ для каждой вершины $$$i$$$ ломаной.
Так как подсчет новых высот может занять много времени, а вы не знаете, когда вас попросят отчитаться, посчитайте наименьшую цену (и соответствующие $$$y_0$$$ и $$$y_1$$$) для выравнивания дороги после получения каждого нового значения $$$b_i$$$.
В первой строке задано одно целое число $$$n$$$ ($$$3 \le n \le 2 \cdot 10^5$$$) — количество вершин ломаной.
Во второй строке заданы $$$n$$$ целых чисел $$$a_0, a_1, \dots, a_{n - 1}$$$ ($$$0 \le a_i \le 10^9$$$; $$$a_0 = a_{n - 1} = 0$$$) — высоты соответствующих вершин.
В третьей строке заданы $$$n$$$ целых чисел $$$b_0, b_1, \dots, b_{n - 1}$$$ ($$$0 \le b_i \le 10^9$$$; $$$b_0 = b_{n - 1} = 0$$$) — новые высоты соответствующих вершин.
Выведите $$$n$$$ чисел: $$$i$$$-м числом ($$$0$$$-индексация) выведите $$$y_0 + y_1$$$ «лучшего отрезка» (т. е. сумму координат отрезка, который имеет минимальную цену), если вы уже знаете новые значения высот $$$b_0, \dots, b_i$$$.
Если существует несколько «лучших отрезков», выведите наименьшее возможное значение $$$y_0 + y_1$$$.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превосходит $$$10^{-9}$$$.
Формально, пусть ваш ответ равен $$$x$$$, а ответ жюри равен $$$y$$$. Ваш ответ будет зачтен, если и только если $$$\frac{|x - y|}{\max{(1, |y|)}} \le 10^{-9}$$$.
50 5 1 3 00 1 3 2 0
8.000000000000 4.000000000000 6.000000000000 6.000000000000 6.000000000000
60 4 1 3 3 00 1 4 0 1 0
7.000000000000 5.000000000000 7.500000000000 7.500000000000 6.666666666667 6.666666666667
Первый ответ на первый пример изображен выше.
Вы можете получить второй ответ, выбрав следующий «лучший отрезок»:
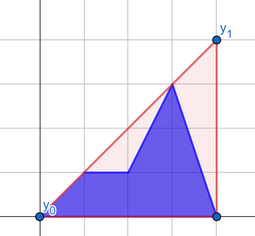
Вы можете достигнуть третий ответ, используя следующий «лучший отрезок»:
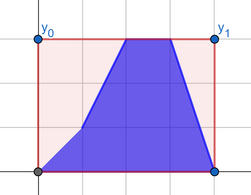
Вы можете получить четвертый ответ следующим образом:
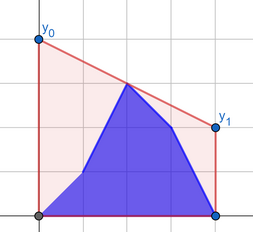
| Название |
|---|




