| Codeforces Round 911 (Div. 2) |
|---|
| Закончено |
Аньи продолжает игнорировать сообщения Кексика. Через общего друга Кексик выяснил, что Аньи очень любит бинарные деревья, и захотел решить ее задачу, чтобы привлечь ее внимание.
Аньи задала Кексику двоичное дерево с $$$n$$$ вершинами. Вершина $$$1$$$ является корнем и не имеет родителя. Все остальные вершины имеют ровно одного родителя. Каждая вершина может иметь до $$$2$$$ детей — левого и правого. Для каждой вершины Аньи сообщает Кексику индекс ее левого и правого ребенка или говорит, что их не существует.
Кроме того, на каждой из вершин написана буква $$$s_i$$$, которая является либо «U», либо «L», либо «R».
Кексик начинает свой путь с корня и на каждом ходу делает следующее:
- Если он находится в вершине, на которой написана буква «U», то он переходит к ее родителю. Если он не существует, то Кексик ничего не делает.
- Если он находится в вершине, на которой написана буква «L», то он переходит к ее левому ребенку. Если его не существует, то он ничего не делает.
- Если он находится в вершине, на которой написана буква «R», то он переходит к ее правому ребенку. Если его не существует, то он ничего не делает.
Перед тем, как отправиться в путь, он может выполнять следующие операции: выбрать любую вершину и заменить написанную на ней букву на другую.
Вас интересует минимальное количество операций, которые он должен выполнить перед путешествием, чтобы, начав путешествие, он в какой-то момент оказался в листе. Лист — это вершина, у которой нет детей. Не имеет значения, какого листа он достигнет. Заметим, что не имеет значения, останется ли он в листе — ему нужно только переместиться в лист. Кроме того, неважно, сколько раз он должен переместиться, прежде чем достигнет листа.
Помогите Кексику решить задачу Аньи, чтобы он смог завоевать ее сердце, и Анья приехала в Чачак.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 5 \cdot 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 3 \cdot 10^5$$$) — количество вершин в дереве.
Вторая строка каждого набора входных данных содержит строку $$$s$$$ длины $$$n$$$ — буквы, написанные на вершинах. Гарантируется, что $$$s$$$ состоит только из букв «U», «L» и «R».
В $$$i$$$-й из следующих $$$n$$$ строк содержатся два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$0 \le l_i, r_i \le n$$$) — индексы левого и правого детей вершины $$$i$$$. Если $$$l_i = 0$$$, то это означает, что вершина $$$i$$$ не имеет левого ребенка. Если $$$r_i = 0$$$, то вершина $$$i$$$ не имеет правого ребенка. Гарантируется, что данные значения задают корректное бинарное дерево с корнем в $$$1$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимальное количество операций, которое необходимо выполнить Кексику, чтобы он смог достичь листа.
53LRU2 30 00 03ULR3 20 00 02LU0 20 04RULR3 00 00 42 07LLRRRLU5 23 60 07 04 00 00 0
0 1 1 3 1
В первом наборе входных данных вершина $$$1$$$ имеет левого ребенка $$$2$$$ и правого — $$$3$$$. Вершины $$$2$$$ и $$$3$$$ не имеют детей и поэтому являются листьями. Поскольку в вершине $$$1$$$ написана буква «L», то Кексик перейдет в вершину $$$2$$$, поэтому ему не нужно выполнять никаких операций.
Во втором наборе входных данных вершина $$$1$$$ имеет левого ребенка $$$3$$$ и правого — $$$2$$$. Вершины $$$2$$$ и $$$3$$$ являются листьями. Поскольку в вершине $$$1$$$ написана буква «U», то для того, чтобы добраться до листа, Кексику необходимо изменить эту букву на «L» или «R».
В третьем наборе вершина $$$1$$$ имеет только правого ребенка, которым является вершина $$$2$$$. Поскольку на корневой вершине написана буква «L», Кексик должен изменить букву на «R», иначе он застрянет в вершине $$$1$$$.
В четвертом наборе он может изменить $$$3$$$ буквы так, чтобы буквы на вершинах были «LURL», что позволит ему достичь вершины $$$2$$$.
В пятом наборе имеется $$$3$$$ листа: $$$3$$$, $$$6$$$ и $$$7$$$. Чтобы добраться до листа $$$6$$$ или листа $$$7$$$, ему нужно поменять $$$2$$$ буквы. Однако, если он поменяет букву на вершине $$$1$$$ на «R», то достигнет листа $$$3$$$, поэтому ответ — $$$1$$$.
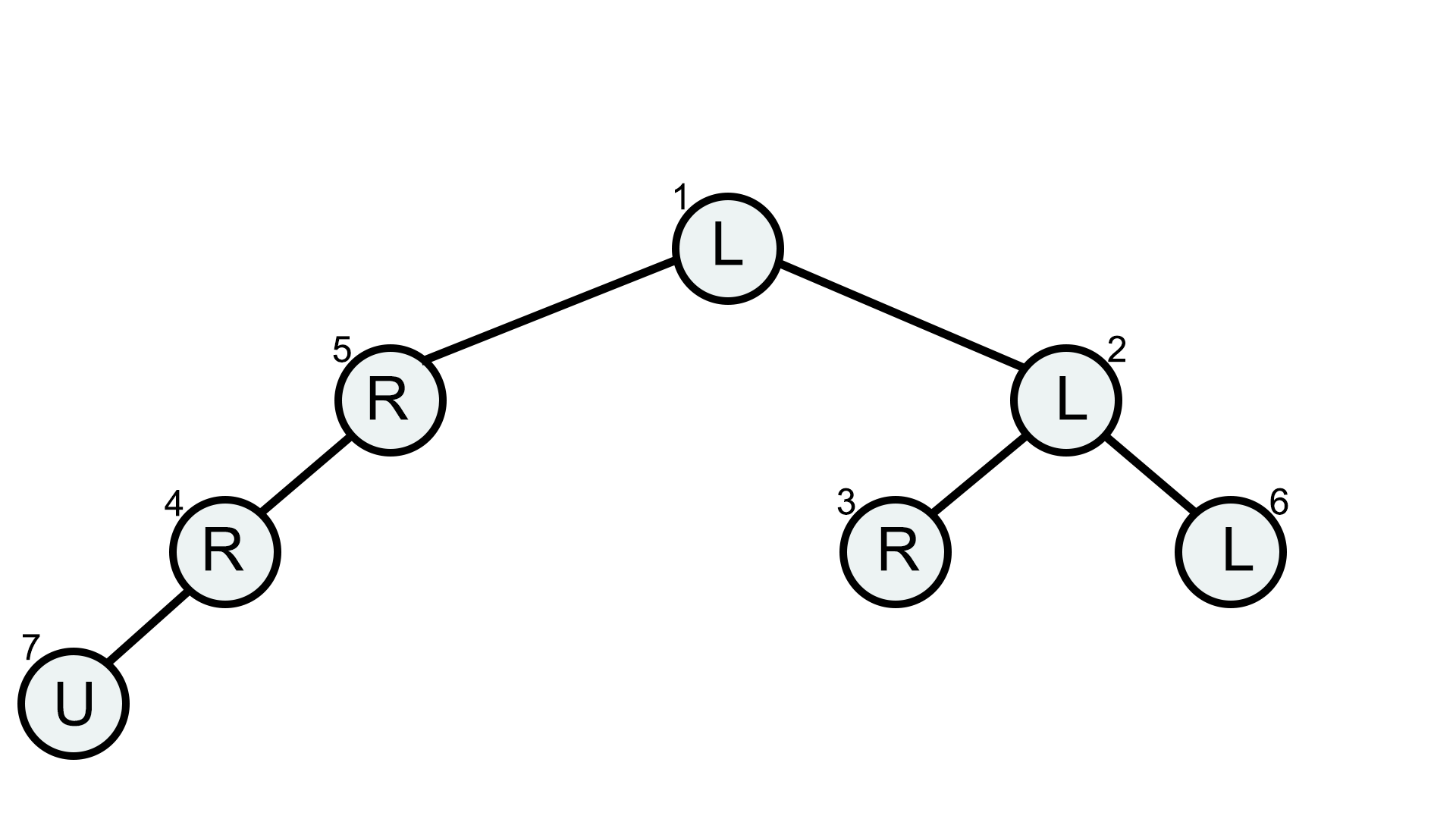 Изначальное дерево в пятом наборе входных данных.
Изначальное дерево в пятом наборе входных данных.
| Название |
|---|




