| Codeforces Round 909 (Div. 3) |
|---|
| Finished |
Tree is a connected graph without cycles. It can be shown that any tree of $$$n$$$ vertices has exactly $$$n - 1$$$ edges.
Leaf is a vertex in the tree with exactly one edge connected to it.
Distance between two vertices $$$u$$$ and $$$v$$$ in a tree is the minimum number of edges that must be passed to come from vertex $$$u$$$ to vertex $$$v$$$.
Alex's birthday is coming up, and Timofey would like to gift him a tree of $$$n$$$ vertices. However, Alex is a very moody boy. Every day for $$$q$$$ days, he will choose an integer, denoted by the integer chosen on the $$$i$$$-th day by $$$d_i$$$. If on the $$$i$$$-th day there are not two leaves in the tree at a distance exactly $$$d_i$$$, Alex will be disappointed.
Timofey decides to gift Alex a designer so that he can change his tree as he wants. Timofey knows that Alex is also lazy (a disaster, not a human being), so at the beginning of every day, he can perform no more than one operation of the following kind:
- Choose vertices $$$u$$$, $$$v_1$$$, and $$$v_2$$$ such that there is an edge between $$$u$$$ and $$$v_1$$$ and no edge between $$$u$$$ and $$$v_2$$$. Then remove the edge between $$$u$$$ and $$$v_1$$$ and add an edge between $$$u$$$ and $$$v_2$$$. This operation cannot be performed if the graph is no longer a tree after it.
Somehow Timofey managed to find out all the $$$d_i$$$. After that, he had another brilliant idea — just in case, make an instruction manual for the set, one that Alex wouldn't be disappointed.
Timofey is not as lazy as Alex, but when he saw the integer $$$n$$$, he quickly lost the desire to develop the instruction and the original tree, so he assigned this task to you. It can be shown that a tree and a sequence of operations satisfying the described conditions always exist.
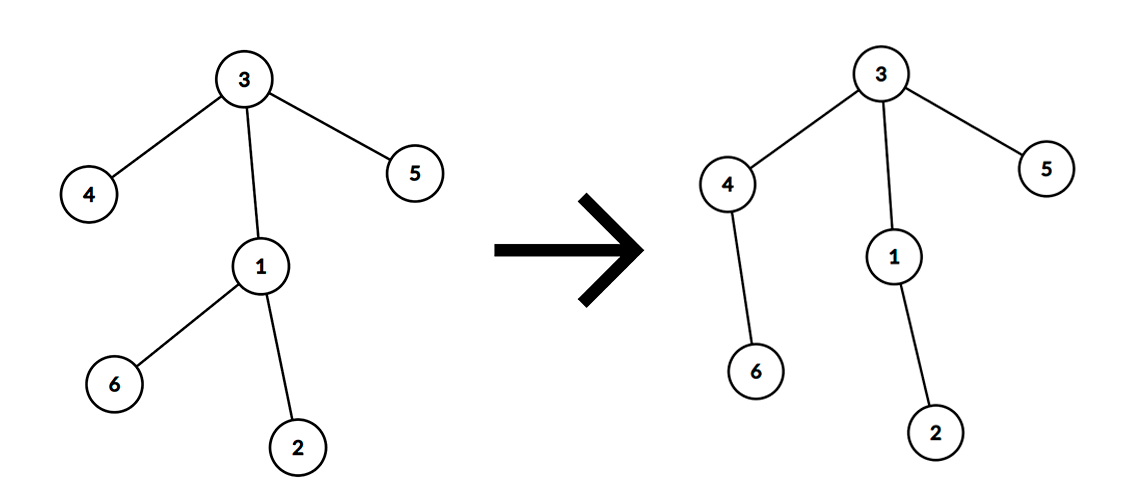
Here is an example of an operation where vertices were selected: $$$u$$$ — $$$6$$$, $$$v_1$$$ — $$$1$$$, $$$v_2$$$ — $$$4$$$.
The first line contains the integer $$$t$$$ ($$$1 \leq t \leq 100$$$) — the number of test cases.
The first line of each test case contains two integers $$$n$$$ ($$$3 \leq n \leq 500$$$) and $$$q$$$ ($$$1 \leq q \leq 500$$$) — the number of nodes in the tree and the number of days, respectively.
The $$$i$$$th of the following $$$q$$$ lines contains the integer $$$d_i$$$ ($$$2 \leq d_i \leq n - 1$$$).
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$500$$$. The same is guaranteed for $$$q$$$.
It can be shown that a tree and a sequence of operations satisfying the described conditions always exist.
For each test case, first print an $$$n - 1$$$ string describing the edges of the tree. If you want the tree to have an edge between nodes $$$u$$$ and $$$v$$$, there must be a string $$$v$$$ $$$u$$$ or $$$u$$$ $$$v$$$ among these $$$n - 1$$$ lines.
In the next $$$q$$$ lines, print three integers each $$$u$$$ $$$v_1$$$ $$$v_2$$$ — a description of the operations. If Alex doesn't need to perform an operation the following day, print $$$-1$$$ $$$-1$$$ $$$-1$$$.
33 32225 64234324 9233222322
1 2 2 3 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 2 2 3 3 4 4 5 -1 -1 -1 4 3 2 5 4 3 4 2 5 4 5 2 5 3 4 1 2 2 3 3 4 4 3 2 4 2 3 -1 -1 -1 4 3 2 -1 -1 -1 -1 -1 -1 4 2 3 4 3 2 -1 -1 -1
| Name |
|---|




