| Codeforces Round 910 (Div. 2) |
|---|
| Закончено |
У Лены есть сетка, образованная $$$n$$$ горизонтальными прямыми и $$$m$$$ вертикальными прямыми. Горизонтальные прямые пронумерованы числами от $$$1$$$ до $$$n$$$ сверху вниз, а вертикальные прямые пронумерованы числами от $$$1$$$ до $$$m$$$ слева направо. Для всех $$$x$$$ и $$$y$$$ ($$$1 \leq x \leq n$$$, $$$1 \leq y \leq m$$$) обозначим за $$$(x, y)$$$ точку пересечения $$$x$$$-й горизонтальной прямой и $$$y$$$-й вертикальной прямой.
Две точки $$$(x_1,y_1)$$$ и $$$(x_2,y_2)$$$ являются соседними тогда и только тогда, когда выполняется $$$|x_1-x_2| + |y_1-y_2| = 1$$$.
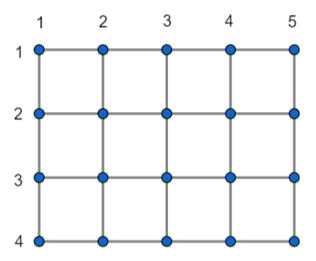 Сетка, образованная $$$n=4$$$ горизонтальными прямыми и $$$m=5$$$ вертикальными прямыми.
Сетка, образованная $$$n=4$$$ горизонтальными прямыми и $$$m=5$$$ вертикальными прямыми. Лена называет последовательность точек $$$p_1, p_2, \ldots, p_g$$$ длины $$$g$$$ путем тогда и только тогда, когда выполняются все следующие условия:
- Первой точкой $$$p_1$$$ в этой последовательности является $$$(1, 1)$$$.
- Последней точкой $$$p_g$$$ в этой последовательности является $$$(n, m)$$$.
- Для всех $$$1 \le i < g$$$ точки $$$p_i$$$ и $$$p_{i+1}$$$ являются соседними.
Обратите внимание, что путь может содержать одну точку несколько раз. В частности, точки $$$(1, 1)$$$ и $$$(n, m)$$$ могут встречаться в пути несколько раз.
Существует $$$n(m-1)+(n-1)m$$$ отрезков, соединяющих соседние точки в Лениной сетке. Лена хочет покрасить каждый из этих отрезков в синий или красный цвет таким образом, что существует путь $$$p_1, p_2, \ldots, p_{k+1}$$$ длины $$$k+1$$$, удовлетворяющая следующему условию:
- среди $$$k$$$ отрезков, соединяющих две последовательные точки в этом пути, никакие два последовательных отрезка не покрашены в один цвет (иными словами, для всех $$$1 \le i < k$$$ цвет отрезка между точками $$$p_i$$$ и $$$p_{i+1}$$$ отличается от цвета отрезка между точками $$$p_{i+1}$$$ и $$$p_{i+2}$$$).
Найдите любую такую раскраску или сообщите, что таких раскрасок не существует.
В первой строке задано одно целое число $$$t$$$ ($$$1 \leq t \leq 32$$$) — количество наборов входных данных. Далее следуют описания этих наборов.
В единственной строке даны три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$3 \leq n,m \leq 16$$$, $$$1 \leq k \leq 10^9$$$) — размеры сетки и количество отрезков в требуемом пути.
Для каждого набора входных данных выведите «NO», если не существует способа покрасить каждый из $$$n(m-1)+(n-1)m$$$ отрезков в синий или красный цвет таким образом, что существует путь длины $$$k+1$$$, удовлетворяющий требованиям из условия.
Иначе выведите «YES», а затем также приведите пример требуемой раскраски.
В каждой из первых $$$n$$$ строк описания раскраски выведите $$$m-1$$$ символ через пробел. $$$j$$$-й символ $$$i$$$-й из этих $$$n$$$ строк должен обозначать цвет отрезка между точками $$$(i,j)$$$ и $$$(i,j+1)$$$. Используйте «B» для обозначения синего цвета и «R» для обозначения красного цвета.
В каждой из следующих $$$n-1$$$ строк описания раскраски выведите $$$m$$$ символов через пробел. $$$j$$$-й символ $$$i$$$-й из этих $$$n-1$$$ строк должен обозначать цвет отрезка между точками $$$(i,j)$$$ и $$$(i+1,j)$$$. Используйте «B» для обозначения синего цвета и «R» для обозначения красного цвета.
Вы можете выводить каждую букву ответа в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ, а обе буквы «R» и «r» приняты как обозначение красного цвета.
54 5 113 3 23 4 10000000003 3 125884 4 8
YES R R B B R R R R B B B R R R B B R B B R B R B B B B B B R R R NO NO YES R B B B B R B B R R B B YES B B R R B R B R R R R B B R R B B B B B B R R R
Одна из корректных раскрасок для первого набора входных данных приведена ниже. Путь длины $$$12$$$, удовлетворяющий требованиям из условия выделен.
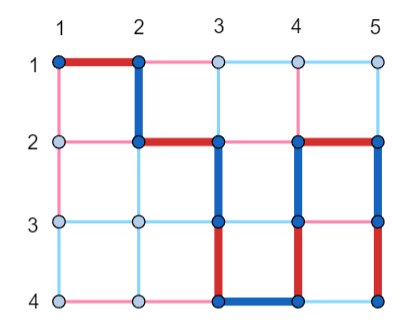
Во втором и третьем наборах входных данных можно показать, что не существует раскрасок, удовлетворяющих требованиям из условия.
| Название |
|---|




