Background
Extended reality (XR) service is a promising application for future communications. In wireless communications, XR data are transmitted over radio between base stations and mobile terminals. A region is usually divided into multiple cells, each of which is equipped with a base station to serve users. One base station usually serves multiple users, and multiple base stations may serve one user at the same time.
Task
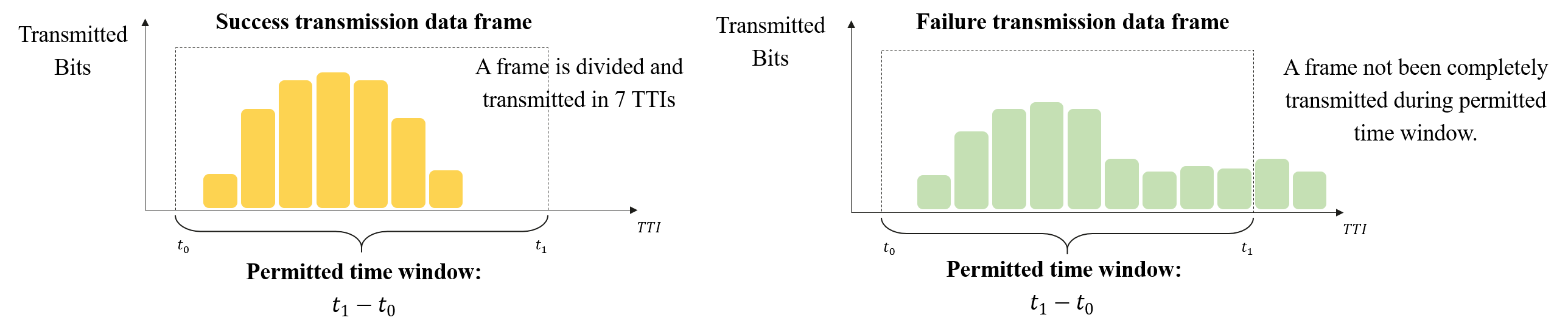
The task of this competition is to design a scheduling algorithm for XR service. By properly allocating radio resources, we want to maximize the number of XR data frames that are successfully transmitted. A diagram is provided below for illustration: The transmission of a data frame is failed when it cannot be completely transmitted during the permitted transmission time window.
Therefore, the objective of this task can be modeled as: $$$$$$ \mathcal{P}: \max \sum_j f_j \tag{1} $$$$$$ $$$$$$ f_j=\left\{\begin{array}{c} 1, g_j \geq T B S_j \\ 0, g_j< T B S_j \end{array}\right. \tag{2} $$$$$$ Here, $$$f_j$$$ represents the transmission result of the $$$j$$$-th frame: when the actual transmitted bits $$$g_j$$$ (computed via (5)) is not less than the size of the frame, i.e., $$$TBS_j$$$ (transport block size), the frame would be successfully transmitted so that $$$f_j=1$$$. Otherwise, $$$f_j=0$$$.
To achieve better user experience, scheduling algorithm should be proposed to efficiently assign the limited radio resources:
- Time domain resource, which is divided into several transmission time intervals (TTIs), each TTI corresponds to a transmission time of $$$0.5$$$ms.
- Frequency domain resource, which is divided into several resource block groups (Resource Block Group, RBG), each RBG corresponds to a transmission bandwidth of $$$5760$$$ kHz.
- Power domain resource: each cell has a fixed maximum transmission power to serve users.
Summarily, two optimization variables are introduced to represent the scheduling result: $$$$$$ b_{r n t}^{(k)} \in\{0,1\} \tag{3} $$$$$$ $$$$$$ p_{ {rnt }}^{(k)} \geq 0 , \quad \sum_r \sum_n p_{ {rnt }}^{(k)} \leq R, \quad \sum_n p_{ {rnt }}^{(k)} \leq 4 \tag{4} $$$$$$ Here, $$$b_{rnt}^{(k)}$$$ is a Boolean variable denoting whether the $$$r$$$-th RBG of cell $$$k$$$ is allocated to user $$$n$$$ at TTI $$$t$$$, and $$$p_{rnt}^{(k)}$$$ is a nonnegative continuous variable denoting the power allocated to user $$$n$$$ in the $$$r$$$-th RBG of cell $$$k$$$ at TTI $$$t$$$. For each TTI of each cell, the power range of each RBG is between $$$0$$$ and $$$4$$$, and the total power of all RBGs can not be larger than $$$R$$$.
When the radio resources are allocated to the users, the XR data transmission can be provided for them. Assume that the $$$j$$$-th frame belongs to the $$$n$$$-th user, the actual transmitted bits for the frame, i.e., $$$g_j$$$ can be given by:
$$$$$$ g_{j}= W\times \sum_{t=t_{0, j}}^{t_{1, j}} \sum_k \sum_r b_{r n t}^{(k)} \times \log _2\left(1+s_{n t}^{(k)}\right). \tag{5} $$$$$$ Note that $$$W\times \mathrm{log}_2 (1+s_{nt}^{(k)} ) $$$ is the well-known Shannon formula, which represents the transmitted data volume, where $$$s_{nt}^{(k)}$$$ represents the transmission SINR (Signal-to-Interference-plus-Noise-Ratio) of user $$$n$$$ in cell $$$k$$$ at TTI $$$t$$$, and $$$W=192$$$ is the constant number of available frequency resounce elements of one RBG. $$$t_{0,j}$$$ and $$$t_{1,j}$$$ denote the start TTI and the end TTI of frame $$$j$$$, respectively. The physical meaning of Formula (5) is that the number of bits transmitted within the valid time period, $$$t_{0,j}\sim t_{1,j}$$$, will be counted as valid transmission bits for the $$$j$$$-th frame.
Finally, we give the expression of SINR, which may be complicated but corresponds to the actual physical transmission:
$$$$$$ s_{nt}^{\left( k \right)} = {\left( {\prod\limits_{r,b_{rnt}^{\left( k \right)} = 1} {s_{rnt}^{\left( k \right)}} } \right)^{\frac{1}{{\sum\nolimits_r {b_{rnt}^{\left( k \right)}} }}}} \tag{6} $$$$$$ $$$$$$ s_{r n t}^{(k)}=\frac{s_{0, r n t}^{(k)} \times p_{r n t}^{(k)} \times \prod_{m \neq n} e^{d^{(k)}_{mrn} \times b_{r m t}^{(k)}}}{1+\sum_{k^{\prime} \neq k, n^{\prime} \neq n} s_{0, r n t}^{(k^{\prime})} \times p_{r n^{\prime} t}^{\left(k^{\prime}\right)} \times e^{-d^{(k^{\prime})}_{n^{\prime}rn}}} \tag{7} $$$$$$
Formula (6) shows the computation of user-level effective SINR: the transmission SINR of user $$$n$$$, i.e., $$$s_{nt}^{(k)}$$$, is the geometric mean of the SINRs of scheduled RBGs. Then, formula (7) shows the computation of RBG-level effective SINR. $$$s_{0,rnt}^{(k)}$$$ is a given constant denoting the initial SINR on RBG $$$r$$$ of cell $$$k$$$ at TTI $$$t$$$, which indicates the quality of the channel. Another given constant value $$$d^{(k)}_{mrn}$$$ represents the interference factor between user $$$m$$$ and user $$$n$$$ on RBG $$$r$$$, when user $$$m$$$ is scheduled on cell $$$k$$$. Note that $$$d^{(k)}_{mrn}=d^{(k)}_{nrm}\le 0$$$, which reveals that scheduling multiple users on the same RBG-TTI resource will cause a decrease in the SINR of each user.
To sum up, participants are required to find an efficient radio resource allocation, so that more XR data frames can be successfully transmitted.
The input of a single test has $$$(4 + R \cdot K \cdot T + N \cdot R \cdot K + 1 + J)$$$ lines, which contains user number $$$N$$$, cell number $$$K$$$, TTI number $$$T$$$, RBG number $$$R$$$, initial SINRs $$$s_{0, r n t}^{(k)}$$$, interference factors $$$d_{mrn}$$$, frame number $$$J$$$ and information about $$$J$$$ frames.
The details are as follows:
- Line $$$1$$$: User number $$$N$$$, integer, $$$1 \leq N \leq 100$$$. Users are numbered from $$$0$$$ to $$$N - 1$$$.
- Line $$$2$$$: Cell number $$$K$$$, integer, $$$1 \leq K \leq 10$$$. Cells are numbered from $$$0$$$ to $$$K - 1$$$.
- Line $$$3$$$: TTI number $$$T$$$, integer, $$$1 \leq T \leq 1000$$$. TTIs are numbered from $$$0$$$ to $$$T - 1$$$.
- Line $$$4$$$: RBG number $$$R$$$, integer, $$$1 \leq R \leq 10$$$. RBGs are numbered from $$$0$$$ to $$$R - 1$$$.
- Line $$$5$$$ to $$$(4+R \cdot K\cdot T)$$$: Initial SINRs $$$s_{0, r n t}^{(k)}$$$, float, $$$0 < s_{0, r n t}^{(k)} < 10\,000$$$. Each line has $$$N$$$ elements, corresponding to $$$N$$$ users. $$$s_{0, r n t}^{(k)}$$$ is the $$$(n+1)$$$-th element of line $$$(5+r+k \cdot R+t \cdot K \cdot R)$$$.
- Line $$$(5+R \cdot K \cdot T)$$$ to $$$(4+R \cdot K \cdot T + N \cdot R \cdot K)$$$: Interference factors $$$d^{(k)}_{mrn}$$$, float, $$$-2 \leq d^{(k)}_{mrn} \leq 0$$$. Each line has $$$N$$$ elements, corresponding to $$$N$$$ users. $$$d^{(k)}_{mrn}$$$ is the $$$(n+1)$$$-th element of line $$$(5+R \cdot K \cdot T+m+r \cdot N + k \cdot R \cdot N)$$$.
- Line $$$(5+R \cdot K \cdot T + N \cdot R \cdot K)$$$: Frame number $$$J$$$, integer, $$$1 \leq J \leq 5000$$$.
- Last $$$J$$$ lines: Frame information. Each line contains $$$5$$$ integers corresponding to a frame, which are, in order: frame ID $$$j\in\{0,\ldots,J-1\}$$$ in increasing order, size $$$TBS_j$$$ ($$$0 < TBS_j \leq 100\,000$$$), user ID it belongs to, first TTI $$$t_{0,j} \in\{0,\ldots,T-1\}$$$, and number of TTIs $$$t_{d,j} \in \left[ {1,100} \right]$$$. Last TTI for frame $$$j$$$ can be found as $$$t_{1,j}=t_{0,j}+t_{d,j}-1$$$; it is guaranteed that $$$t_{1,j} \le T - 1$$$.
Output for a certain input is the optimization result of $$$p_{r n t}^{(k)}$$$ (float), which has $$$R \cdot K \cdot T$$$ lines. Each line has $$$N$$$ elements, corresponding to $$$N$$$ users. $$$p_{r n t}^{(k)}$$$ is the $$$(n+1)$$$-th element of line $$$(1+r+k \cdot R+t \cdot K \cdot R)$$$.
Note that the optimization result of $$$b_{r n t}^{(k)}$$$ does not need to be output, because $$$p_{r n t}^{(k)}>0$$$ and $$$p_{r n t}^{(k)} = 0$$$ means $$$b_{r n t}^{(k)}=1$$$ and $$$b_{r n t}^{(k)} = 0$$$, respectively.
Please note that if the outputs do not meet the constraint (4), it will be judged as an incorrect answer and get score $$$0$$$. Besides, transmit on some TTIs out of time window is valid, but usually results in a lower score due to resources waste.
The goal is to maximize the number of successfully scheduled frames. When these numbers are tied, we will compare who used less power. To achieve that, $$$Score = X - 10^{-6}\times p$$$, where $$$X$$$ and $$$p$$$ represent the number of successfully scheduled frames and the total power used for transmission, respectively.
The total score for a submission is the sum of scores on each test.
2 2 2 1 1.3865 11.3865 1.3865 11.3865 2.3865 2.3865 2.3865 2.3865 0 -2 -2 0 0 -2 -2 0 2 0 250 0 0 2 1 25 1 0 2
0.000000 0.004950 0.000000 0.004950 0.245039 0.000000 0.245039 0.000000
Two sets of tests are prepared in this problem. For the duration of the competition, each submission is tested on the preliminary set of tests. When the competition is finished, for each contestant:
The jury takes the latest submission with non-zero score on preliminary tests;
This submission is tested on the final set of tests for the final rank;
The two sets of tests are generated from the same pool of data, based on the real word data.
| Name |
|---|




