| Codeforces Round 903 (Div. 3) |
|---|
| Закончено |
У вас есть дерево из $$$n$$$ вершин, некоторые вершины которого помечены. Дерево — это связный неориентированный граф без циклов.
Обозначим за $$$f_i$$$ максимальное расстояние от вершины с номером $$$i$$$ до какой-то из помеченных вершин.
Ваша задача — найти минимальное значение $$$f_i$$$ среди всех вершин.
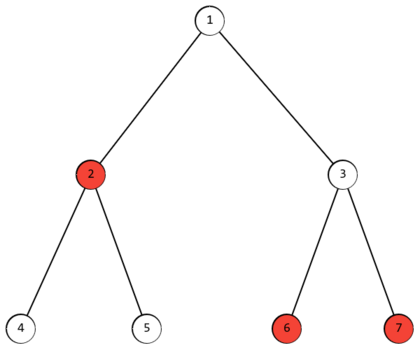
Например, в дереве из примера раскрашены вершины с номерами $$$2$$$, $$$6$$$ и $$$7$$$. Тогда массив $$$f(i) = [2, 3, 2, 4, 4, 3, 3]$$$. $$$f_i$$$ минимальна для вершин с номерами $$$1$$$ и $$$3$$$.
В первой строке записано число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных записаны два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le k \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве и количество помеченных вершин соответственно.
Во второй строке каждого набора входных данных записаны $$$k$$$ целых чисел $$$a_i$$$ ($$$1 \le a_i \le n, a_{i-1} < a_i$$$) — номера помеченных вершин.
Следующие $$$n - 1$$$ строк содержат по два челых числа $$$u_i$$$ и $$$v_i$$$ — номера вершин, соединяемых $$$i$$$-м ребром.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимальное значение $$$f_i$$$ по всем вершинам.
67 32 6 71 21 32 42 53 63 74 41 2 3 41 22 33 45 111 21 31 41 55 24 51 22 31 44 510 81 2 3 4 5 8 9 102 1010 55 33 11 77 44 98 96 110 91 2 4 5 6 7 8 9 101 33 99 44 1010 66 77 22 55 8
2 2 0 1 4 5
36 131 21 33 43 52 65 31 2 51 21 32 43 57 123 22 66 15 67 64 5
0 2 0
| Название |
|---|




