| Codeforces Round 898 (Div. 4) |
|---|
| Закончено |
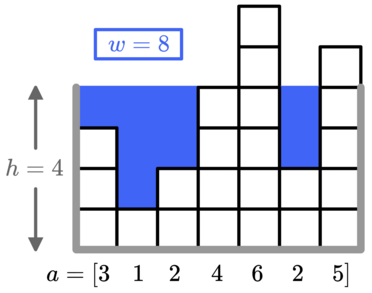
Вы любите рыб, поэтому решили построить аквариум. У вас есть кусок коралла, состоящий из $$$n$$$ колонн, $$$i$$$-я из которых имеет высоту $$$a_i$$$ единиц. Затем вы построите вокруг коралла аквариум следующим образом:
- Выберите целое число $$$h \geq 1$$$ — высоту аквариума. Постройте стены высотой $$$h$$$ с обеих сторон аквариума.
- Затем заполните аквариум водой так, чтобы высота каждой колонны была равна $$$h$$$, если только коралл не выше $$$h$$$; в этом случае в эту колонну вода добавляться не должна.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора содержит два положительных целых числа $$$n$$$ и $$$x$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$; $$$1 \leq x \leq 10^9$$$) — количество колонн коралла и максимальное количество воды, которое вы можете использовать.
Вторая строка каждого набора содержит $$$n$$$ целых чисел, разделенных пробелом, $$$a_i$$$ ($$$1 \leq a_i \leq 10^9$$$) — высоты колонн коралла.
Сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно положительное целое число $$$h$$$ ($$$h \geq 1$$$) — максимальную высоту аквариума, для заполнения которого вам потребуется не более $$$x$$$ единиц воды.
Можно доказать, что при таких ограничениях всегда существует такое значение $$$h$$$.
57 93 1 2 4 6 2 53 101 1 14 11 4 3 46 19842 6 5 9 1 81 10000000001
4 4 2 335 1000000001
Первый пример изображен в условии. С $$$h=4$$$ нам потребуется $$$8$$$ единиц воды, но если увеличить $$$h$$$ до $$$5$$$, нам потребуется $$$13$$$ единиц воды, что больше, чем $$$x=9$$$. Поэтому оптимальное значение $$$h=4$$$.
Во втором примере случае мы можем выбрать $$$h=4$$$ и добавить $$$3$$$ единицы к каждой колонне, используя в общей сложности $$$9$$$ единиц воды. Можно показать, что это оптимально.
В третьем примере случае мы можем выбрать $$$h=2$$$ и использовать всю нашу воду, поэтому это оптимально.
| Название |
|---|




