| Codeforces Round 896 (Div. 1) |
|---|
| Закончено |
Псевдодеревом называется связный граф, который имеет ровно один цикл и не имеет петель. Обратите внимание, что псевдодерево может содержать кратные рёбра. Можно доказать, что псевдодерево с $$$n$$$ вершинами всегда содержит $$$n$$$ рёбер.
После удаления всех рёбер на цикле в псевдодереве образуется лес$$$^{\dagger}$$$. Можно доказать, что каждое дерево в лесу будет содержать ровно одну вершину, которая находится на цикле до удаления рёбер. Если все деревья в лесу имеют одинаковую глубину$$$^{\ddagger}$$$ при выборе вершины на цикле в качестве корня, мы называем исходное псевдодерево цветочным.
У нашего друга sszcdjr, было цветочное псевдодерево с $$$n$$$ вершинами и $$$n$$$ рёбрами. Однако, он забыл все рёбра в псевдодереве. К счастью, он все ещё помнит степени вершин. В частности, степень $$$i$$$-й вершины равна $$$d_i$$$.
Вы должны помочь sszcdjr построить возможное цветочное псевдодерево с $$$n$$$ вершинами, где степень $$$i$$$-й вершины строго равна $$$d_i$$$, или сообщить ему, что это невозможно.
$$$^{\dagger}$$$ Лесом называется граф, в котором все компоненты связности являются деревьями. Деревом называется связный граф без циклов и петель.
$$$^{\ddagger}$$$ Глубиной дерева с корнем называется максимальное расстояние от корня до вершины этого дерева.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1\leq t\leq 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2\leq n\leq 10^6$$$) — количество вершин.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$d_1,d_2,\ldots,d_n$$$ ($$$1\leq d_i\leq n$$$) — степень каждой вершины.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$10^6$$$.
Для каждого набора входных данных, если существует возможное цветочное псевдодерево:
- Выведите «Yes» (без кавычек) в первой строке.
- Затем выведите $$$n$$$ строк, в каждой строке выведите два целых числа $$$u_i$$$ и $$$v_i$$$ — две вершины, которые соединяет $$$i$$$-е ребро.
Если есть несколько ответов, вы можете вывести любой из них.
В противном случае, выведите «No» (без кавычек) в единственной строке вывода.
Вы можете выводить первую строку для каждого набора входных данных в любом регистре (верхнем или нижнем). Например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительные ответы.
632 2 241 2 3 474 3 3 1 1 1 161 1 2 2 3 3101 1 5 2 1 1 1 1 1 691 1 3 1 1 4 1 1 5
Yes 1 2 2 3 3 1 No Yes 1 2 2 3 3 1 1 4 1 5 2 6 3 7 Yes 5 6 6 5 1 3 2 4 3 5 4 6 No Yes 3 6 6 9 9 3 1 3 2 6 4 6 5 9 7 9 8 9
В первом наборе входных данных единственным возможным цветочным псевдодеревом является:
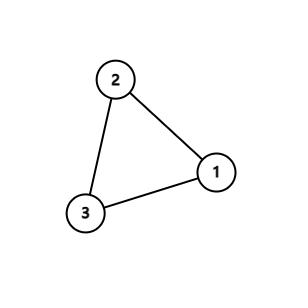
После удаления всех рёбер на цикле в псевдодереве каждое дерево имеет глубину $$$0$$$.
Во втором наборе входных данных можно доказать, что не существует такого цветочного псевдодерева.
В третьем наборе входных данных одним из возможных цветочных псевдодеревьев является:
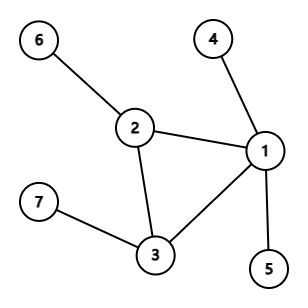
| Название |
|---|




