| Codeforces Round 896 (Div. 1) |
|---|
| Закончено |
Во время летних каникул после экзамена, Tom и Daniel планировали отправиться в путешествие.
В их стране есть $$$n$$$ городов, пронумерованных от $$$1$$$ до $$$n$$$. И система дорожного движения в стране особенная. Для любого города $$$i$$$ ($$$1 \le i \le n$$$) есть:
- дорога между городами $$$i$$$ и $$$2i$$$, если $$$2i\le n$$$;
- дорога между городами $$$i$$$ и $$$2i+1$$$, если $$$2i+1\le n$$$.
Составляя план путешествия, Daniel выбирает некоторое целое значение от $$$1$$$ до $$$m$$$ для каждого города, для $$$i$$$-го города обозначим его $$$a_i$$$.
Пусть $$$s_{i,j}$$$ равно максимальному значению для городов на простом$$$^\dagger$$$ пути между городами $$$i$$$ и $$$j$$$. Тогда оценка плана путешествия равна $$$\sum_{i=1}^n\sum_{j=i}^n s_{i,j}$$$.
Tom хочет знать сумму оценок всех возможных планов путешествия. Daniel просит вас помочь ему найти её. Вам нужно сказать ответ по модулю $$$998\,244\,353$$$.
$$$^\dagger$$$ Простым путём между городами $$$x$$$ и $$$y$$$ называется путь между ними, который проходит по каждому городу не более одного раза.
Первая строка входных данных содержит единственное целое число $$$t$$$ ($$$1\le t\le 200$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Единственная строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1\leq n\leq 10^{18}$$$, $$$1\leq m\leq 10^5$$$) — количество городов и максимальное значение для города.
Гарантируется, что сумма $$$m$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите одно целое число — сумму оценок всех возможных планов путешествия по модулю $$$998\,244\,353$$$.
53 12 210 943 20154 147
6 19 583217643 68816635 714002110
В первом наборе входных данных есть только один возможный план путешествия:
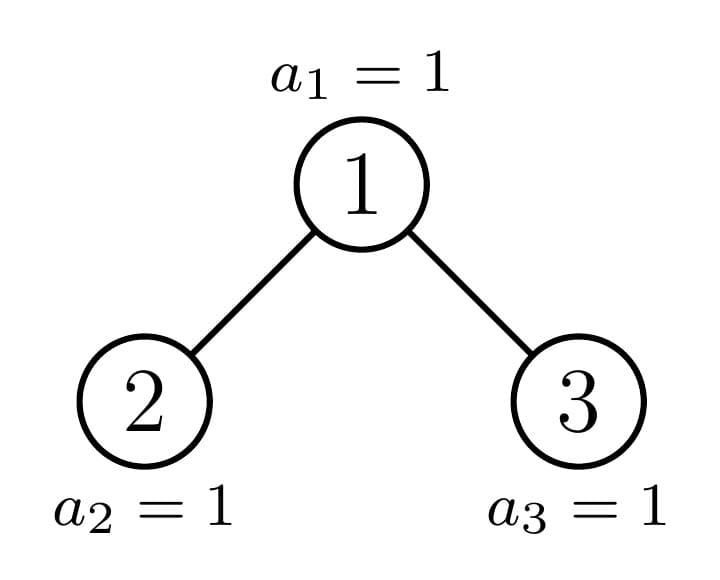
Путь $$$1\rightarrow 1$$$: $$$s_{1,1}=a_1=1$$$.
Путь $$$1\rightarrow 2$$$: $$$s_{1,2}=\max(1,1)=1$$$.
Путь $$$1\rightarrow 3$$$: $$$s_{1,3}=\max(1,1)=1$$$.
Путь $$$2\rightarrow 2$$$: $$$s_{2,2}=a_2=1$$$.
Путь $$$2\rightarrow 1\rightarrow 3$$$: $$$s_{2,3}=\max(1,1,1)=1$$$.
Путь $$$3\rightarrow 3$$$: $$$s_{3,3}=a_3=1$$$.
Оценка равна $$$1+1+1+1+1+1=6$$$.
Во втором наборе входных данных есть четыре возможных плана путешествия:
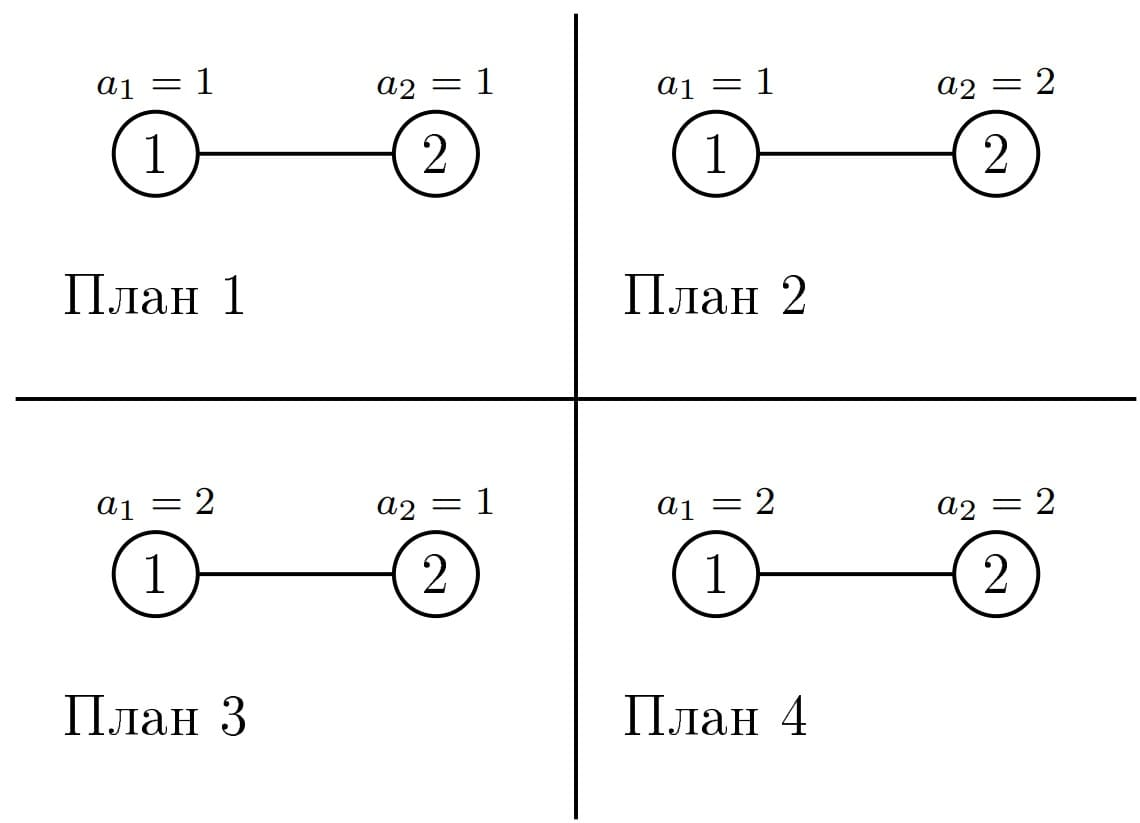
Оценка плана $$$1$$$: $$$1+1+1=3$$$.
Оценка плана $$$2$$$: $$$1+2+2=5$$$.
Оценка плана $$$3$$$: $$$2+2+1=5$$$.
Оценка плана $$$4$$$: $$$2+2+2=6$$$.
Таким образом, сумма оценок равна $$$3+5+5+6=19$$$.
| Название |
|---|




