Это простая версия задачи. Различия между двумя версиями заключаются в ограничении на $$$n$$$ и ограничении по времени. Делать взломы можно только в том случае, если решены обе версии задачи.
Дано дерево с $$$n$$$ вершинами с корнем в вершине $$$1$$$.
Для некоторой перестановки$$$^\dagger$$$ $$$a$$$ длины $$$n$$$ пусть $$$f(a)$$$ — количество пар вершин $$$(u, v)$$$ таких, что $$$a_u < a_{\operatorname{lca}(u, v)} < a_v$$$. Здесь $$$\operatorname{lca}(u,v)$$$ обозначает наименьшего общего предка вершин $$$u$$$ и $$$v$$$.
Найдите максимально возможное значение $$$f(a)$$$ по всем перестановкам $$$a$$$ длины $$$n$$$.
$$$^\dagger$$$ Перестановкой длины $$$n$$$ является массив, состоящий из $$$n$$$ различных целых чисел от $$$1$$$ до $$$n$$$ в произвольном порядке. Например, $$$[2,3,1,5,4]$$$ — перестановка, но $$$[1,2,2]$$$ не перестановка ($$$2$$$ встречается в массиве дважды) и $$$[1,3,4]$$$ тоже не перестановка ($$$n=3$$$, но в массиве встречается $$$4$$$).
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 5000$$$) — количество вершин в дереве.
Вторая строка содержит $$$n - 1$$$ целых чисел $$$p_2,p_3,\ldots,p_n$$$ ($$$1 \le p_i < i$$$), указывающих на наличие ребра между вершинами $$$i$$$ и $$$p_i$$$.
Выведите максимальное значение $$$f(a)$$$.
5 1 1 3 3
4
2 1
0
6 1 2 2 1 5
7
4 1 1 1
2
Дерево в первом примере:
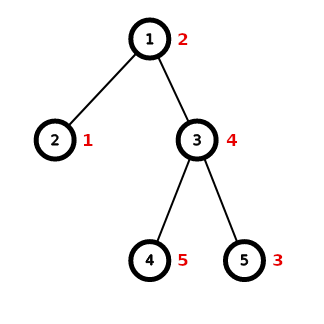
Одной возможной оптимальной перестановкой $$$a$$$ является $$$[2, 1, 4, 5, 3]$$$ с $$$4$$$-мя подходящими парами вершин:
- $$$(2, 3)$$$, так как $$$\operatorname{lca}(2, 3) = 1$$$ и $$$1 < 2 < 4$$$,
- $$$(2, 4)$$$, так как $$$\operatorname{lca}(2, 4) = 1$$$ и $$$1 < 2 < 5$$$,
- $$$(2, 5)$$$, так как $$$\operatorname{lca}(2, 5) = 1$$$ и $$$1 < 2 < 3$$$,
- $$$(5, 4)$$$, так как $$$\operatorname{lca}(5, 4) = 3$$$ и $$$3 < 4 < 5$$$.
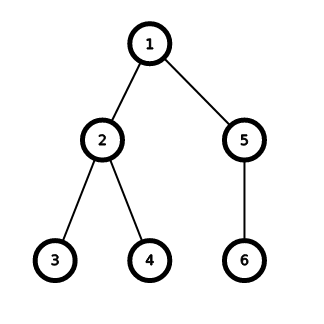
Дерево в третьем примере:
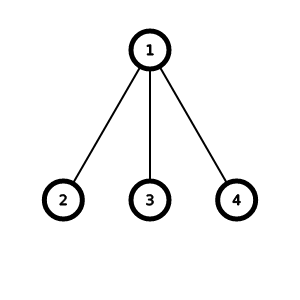
Дерево в четвёртом примере:
| Название |
|---|




