| Codeforces Round 886 (Div. 4) |
|---|
| Закончено |
Компас указывает прямо на утреннюю звезду. Он может указывать только в одном из восьми направлений: четыре основных направления (N, S, E, W) или их комбинации (NW, NE, SW, SE). В противном случае, он сломается.
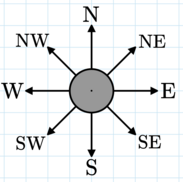 Направления, в которых может указывать компас.
Направления, в которых может указывать компас. На плоскости находится $$$n$$$ различных точек с целочисленными координатами. Сколько существует способов разместить компас в одной точке и утреннюю звезду в другой, чтобы компас не сломался?
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^4$$$). Затем следуют описания наборов.
Первая строка каждого набора содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — количество точек.
Затем следуют $$$n$$$ строк, каждая строка содержит два целых числа $$$x_i$$$, $$$y_i$$$ ($$$-10^9 \leq x_i, y_i \leq 10^9$$$) — координаты каждой точки.
Гарантируется, что сумма $$$n$$$ по всем тестовым случаям не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — количество пар точек, которые не сломают компас.
530 0-1 -11 144 55 76 910 133-1000000000 10000000000 01000000000 -100000000050 02 2-1 5-1 102 1130 0-1 21 -2
6 2 6 8 0
В первом примере, любая пара точек не сломает компас:
- Компас находится в $$$(0,0)$$$, утренняя звезда находится в $$$(-1,-1)$$$: компас будет указывать $$$\text{SW}$$$.
- Компас находится в $$$(0,0)$$$, утренняя звезда находится в $$$(1,1)$$$: компас будет указывать $$$\text{NE}$$$.
- Компас находится в $$$(-1,-1)$$$, утренняя звезда находится в $$$(0,0)$$$: компас будет указывать $$$\text{NE}$$$.
- Компас находится в $$$(-1,-1)$$$, утренняя звезда находится в $$$(1,1)$$$: компас будет указывать $$$\text{NE}$$$.
- Компас находится в $$$(1,1)$$$, утренняя звезда находится в $$$(0,0)$$$: компас будет указывать $$$\text{SW}$$$.
- Компас находится в $$$(1,1)$$$, утренняя звезда находится в $$$(-1,-1)$$$: компас будет указывать $$$\text{SW}$$$.
Во втором примере, только две пары точек не сломают компас:
- Компас находится в $$$(6,9)$$$, утренняя звезда находится в $$$(10,13)$$$: компас будет указывать $$$\text{NE}$$$.
- Компас находится в $$$(10,13)$$$, утренняя звезда находится в $$$(6,9)$$$: компас будет указывать $$$\text{SW}$$$.
| Название |
|---|




