| Codeforces Round 886 (Div. 4) |
|---|
| Закончено |
У Мирчи есть $$$n$$$ картин. $$$i$$$-я картина является квадратом со стороной $$$s_i$$$ сантиметров.
Он прикрепил каждую картину к квадратному куску картона так, чтобы у каждой картинки был картон шириной $$$w$$$ сантиметров со всех сторон. Всего он использовал $$$c$$$ квадратных сантиметров картона. Зная размеры картин и значение $$$c$$$, сможете ли вы найти значение $$$w$$$?
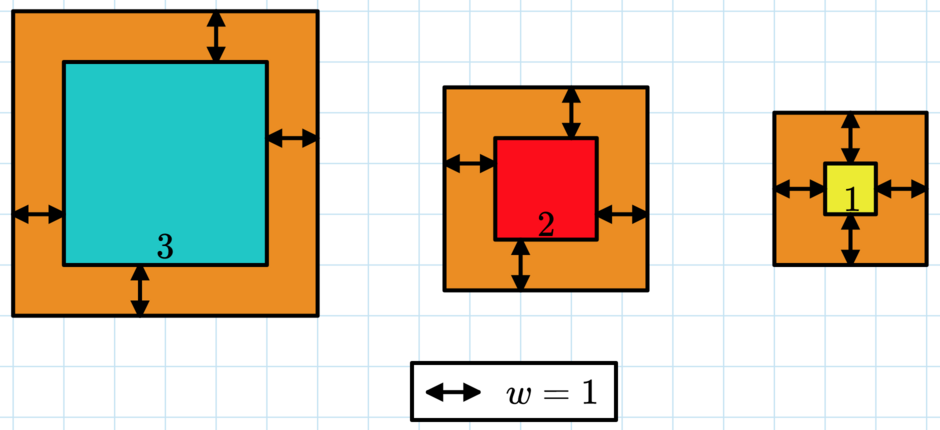Картинка первого тестового примера. Здесь $$$c = 50 = 5^2 + 4^2 + 3^2$$$, поэтому ответ $$$w=1$$$. Обратите внимание, что кусок картона находится за каждой картинкой, а не только по краям.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных.
Первая строка каждого набора содержит два положительных целых числа $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) и $$$c$$$ ($$$1 \leq c \leq 10^{18}$$$) — количество картин и количество использованных квадратных сантиметров картона.
Вторая строка каждого набора содержит $$$n$$$ целых чисел, разделенных пробелами, $$$s_i$$$ ($$$1 \leq s_i \leq 10^4$$$) — размеры картин.
Сумма $$$n$$$ по всем наборам не превышает $$$2 \cdot 10^5$$$.
Дополнительное ограничение на ввод: Для каждого набора входных данных существует такое целое число $$$w$$$.
Пожалуйста, обратите внимание, что некоторые наборы входных данных могут не поместиться в 32-разрядный целочисленный тип, поэтому вам следует использовать по крайней мере 64-разрядный целочисленный тип в вашем языке программирования (например, long long для C++).
Для каждого набора входных данных выведите одно целое число — значение $$$w$$$ ($$$w \geq 1$$$), при котором понадобится ровно $$$c$$$ квадратных сантиметров картона.
10 3 50 3 2 1 1 100 6 5 500 2 2 2 2 2 2 365 3 4 2 469077255466389 10000 2023 10 635472106413848880 9181 4243 7777 1859 2017 4397 14 9390 2245 7225 7 176345687772781240 9202 9407 9229 6257 7743 5738 7966 14 865563946464579627 3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384 19 977162053008871403 9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161 18 886531871815571953 2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764
1 2 4 5 7654321 126040443 79356352 124321725 113385729 110961227
Первый пример объяснен в условии.
Для второго примера выбрано значение $$$w$$$ равное $$$2$$$, таким образом, площадь, покрытая картоном, составляет $$$c = (2 \cdot 2 + 6)^2 = 10^2 = 100$$$ квадратных сантиметров.
Для третьего примера выбрано значение $$$w$$$ равное $$$4$$$, что дает площадь покрытия $$$c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$$$ квадратных сантиметров.
