There are $$$n$$$ pairwise-distinct points and a line $$$x+y=k$$$ on a two-dimensional plane. The $$$i$$$-th point is at $$$(x_i,y_i)$$$. All points have non-negative coordinates and are strictly below the line. Alternatively, $$$0 \leq x_i,y_i, x_i+y_i < k$$$.
Tenzing wants to erase all the points. He can perform the following two operations:
- Draw triangle: Tenzing will choose two non-negative integers $$$a$$$, $$$b$$$ that satisfy $$$a+b<k$$$, then all points inside the triangle formed by lines $$$x=a$$$, $$$y=b$$$ and $$$x+y=k$$$ will be erased. It can be shown that this triangle is an isosceles right triangle. Let the side lengths of the triangle be $$$l$$$, $$$l$$$ and $$$\sqrt 2 l$$$ respectively. Then, the cost of this operation is $$$l \cdot A$$$.
The blue area of the following picture describes the triangle with $$$a=1,b=1$$$ with cost $$$=1\cdot A$$$.

- Erase a specific point: Tenzing will choose an integer $$$i$$$ that satisfies $$$1 \leq i \leq n$$$ and erase the point $$$i$$$. The cost of this operation is $$$c_i$$$.
Help Tenzing find the minimum cost to erase all of the points.
The first line of the input contains three integers $$$n$$$, $$$k$$$ and $$$A$$$ ($$$1\leq n,k\leq 2\cdot 10^5$$$, $$$1\leq A\leq 10^4$$$) — the number of points, the coefficient describing the hypotenuse of the triangle and the coefficient describing the cost of drawing a triangle.
The following $$$n$$$ lines of the input the $$$i$$$-th line contains three integers $$$x_i,y_i,c_i$$$ ($$$0\leq x_i,y_i,x_i+y_i< k$$$, $$$1\leq c_i\leq 10^4$$$) — the coordinate of the $$$i$$$-th points and the cost of erasing it using the second operation. It is guaranteed that the coordinates are pairwise distinct.
Output a single integer —the minimum cost needed to erase all of the points.
4 6 1 1 2 1 2 1 1 1 1 1 3 2 6
4
6 7 1 4 2 1 3 3 1 5 1 4 3 2 5 4 1 1 0 6 4
4
10 4 100 0 0 1 0 1 1 0 2 50 0 3 200 1 0 1 1 1 1 1 2 1 2 0 200 2 1 200 3 0 200
355
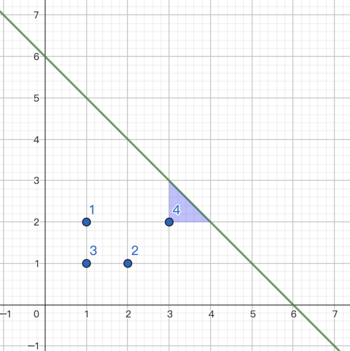
The picture of the first example:
Tenzing do the following operations:
- draw a triangle with $$$a=3,b=2$$$, the cost $$$=1\cdot A=1$$$.
- erase the first point, the cost $$$=1$$$.
- erase the second point, the cost $$$=1$$$.
- erase the third point, the cost $$$=1$$$.
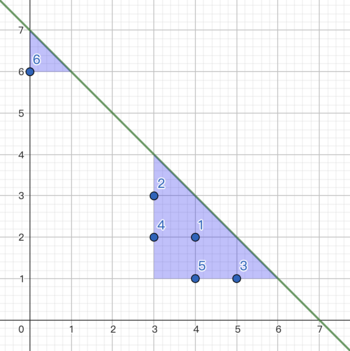
The picture of the second example:
| Name |
|---|




