| Codeforces Round 874 (Div. 3) |
|---|
| Закончено |
У Ксюши есть домашняя шиншилла, дерево на $$$n$$$ вершинах и огромные ножницы. Деревом называется связный граф без циклов. Сейчас Ксюша сидит на скучном уроке физики и думает над тем, как развлечь своего питомца.
Шиншиллам нравится играть с веточками. Веточкой называется дерево из $$$3$$$ вершин.
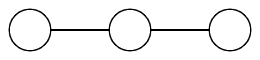 Веточка выглядит так.
Веточка выглядит так. Разрезом называется удаление некоторого (ещё не отрезанного) ребра в дереве. У Ксюши полно свободного времени, поэтому она может себе позволить сделать достаточно разрезов, чтобы дерево распалось на веточки. Другими словами, после нескольких (возможно нуля) разрезов, каждая вершина должна принадлежать ровно одной веточке.
Помогите Ксюше выбрать отрезаемые рёбра или сообщите, что сделать это невозможно.
В первой строке дано единственное целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных дано единственное целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Следующие $$$n - 1$$$ строк каждого набора входных данных содержат целые числа $$$v_i$$$ и $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$) — номера вершин, которые соединяет $$$i$$$-е ребро.
Гарантируется, что данный набор рёбер образует дерево. Также гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Выведите ответ для каждого набора входных данных.
Если искомого способа разрезать дерево не существует, выведите $$$-1$$$.
В противном случае выведите целое число $$$k$$$ — количество отрезаемых рёбер. В следующей строке выведите $$$k$$$ различных целых чисел $$$e_i$$$ ($$$1 \le e_i < n$$$) — номера отрезаемых рёбер. Если $$$k = 0$$$, выведите вместо этого пустую строку.
Если решений несколько, вы можете вывести любое.
491 24 37 95 44 63 28 71 761 21 34 31 56 161 23 23 44 56 551 35 35 23 4
2 2 8 -1 1 3 -1
421 231 23 161 23 13 43 56 192 66 99 19 71 87 38 54 7
-1 0 1 2 2 4 3
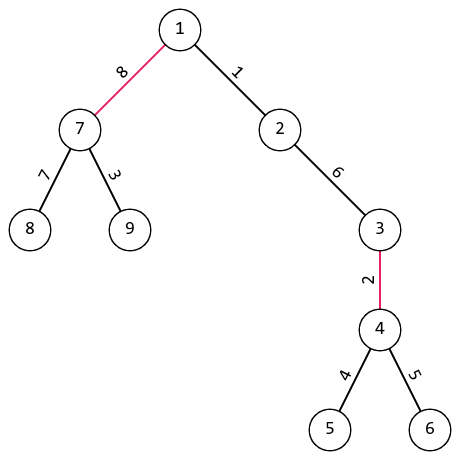 Первый набор входных данных в первом тесте.
Первый набор входных данных в первом тесте.
| Название |
|---|




