| Codeforces Round 873 (Div. 1) |
|---|
| Закончено |
Вам задано дерево (неориентированный связный ациклический граф), изначально содержащее только вершину $$$1$$$. Будет несколько запросов к данному дереву. В $$$i$$$-м запросе появится вершина $$$i + 1$$$, соединенная с вершиной $$$p_i$$$ ($$$1 \le p_i \le i$$$).
После каждого запроса найдите наименьшее количество операций, необходимых для того, чтобы текущее дерево имело два центроида. За одну операцию вы можете добавить одну вершину и одно ребро к дереву так, чтобы оно осталось деревом.
Вершина называется центроидом, если ее удаление разбивает дерево на поддеревья с не более чем $$$\lfloor \frac{n}{2} \rfloor$$$ вершин в каждом, где $$$n$$$ — число вершин дерева. Например, центроид следующего дерева равен $$$3$$$, потому что самое большое поддерево после удаления центроида имеет $$$2$$$ вершины.

В следующем дереве вершины $$$1$$$ и $$$2$$$ являются центроидами.
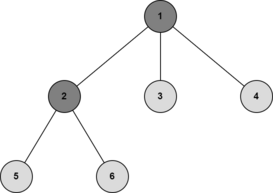
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^4$$$). Далее следует их описание.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 5 \cdot 10^{5}$$$) — количество вершин конечного дерева.
Вторая строка каждого набора входных данных содержит $$$n - 1$$$ целое число $$$p_1, p_2, \ldots, p_{n - 1}$$$ ($$$1 \le p_i \le i$$$) — индекс вершины, которая связана с вершиной $$$i + 1$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$5 \cdot 10^{5}$$$.
Для каждого набора входных данных выведите $$$n - 1$$$ целое число. $$$i$$$-е число является ответом на $$$i$$$-й запрос — наименьшее количество операций, необходимых для того, чтобы текущее дерево имело два центроида.
Мы можем показать, что ответ всегда существует.
52131 141 2 371 2 3 2 5 2101 2 2 4 5 5 7 8 9
0 0 1 0 1 0 0 1 0 1 2 3 0 1 2 1 0 1 0 1 2
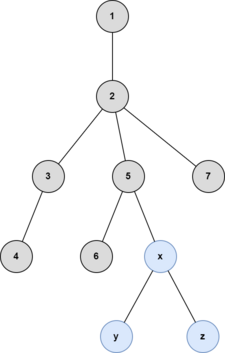
На картинках ниже показан четвертый набор входных данных.
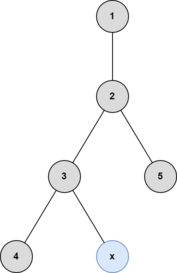
После третьего запроса:
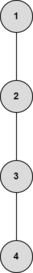
После четвертого запроса:
После пятого запроса:
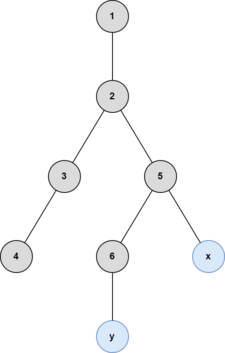
После шестого запроса:
| Название |
|---|




