| Codeforces Round 872 (Div. 1) |
|---|
| Закончено |
LuoTianyi смотрит аниме Made in Abyss. Она считает, что создание Картриджа является очень интересным занятием. Чтобы более четко описать процесс создания Картриджа, она абстрагируется от исходной задачи и даёт вам следующую.
Вам дано дерево $$$T$$$, состоящее из $$$n$$$ вершин. Каждая вершина имеет значения $$$a_i$$$ и $$$b_i$$$, а каждое ребро имеет значения $$$c_j$$$ и $$$d_j$$$.
Теперь вам нужно построить дерево $$$T'$$$ следующим образом:
- Сначала выберите $$$p$$$ вершин из $$$T$$$ ($$$p$$$ — число, выбранное вами самостоятельно) в качестве множества вершин $$$S'$$$ в $$$T'$$$;
- Затем последовательно выберите $$$p-1$$$ ребро из $$$T$$$ по одному (нельзя выбирать одно ребро более одного раза);
- Пусть вы выбрали $$$j$$$-е ребро, и оно соединяет вершины $$$x_j$$$ и $$$y_j$$$ и имеет значения $$$(c_j,d_j)$$$. Тогда вы можете выбрать две вершины $$$u$$$ и $$$v$$$ в $$$S'$$$, для которых ребро $$$(x_j,y_j)$$$ лежит на простом пути из $$$u$$$ в $$$v$$$ в $$$T$$$, и соединить $$$u$$$ и $$$v$$$ в $$$T'$$$ ребром со значениями $$$(c_j,d_j)$$$ ($$$u$$$ и $$$v$$$ не должны содержаться в одной компоненте связности ранее в $$$T'$$$).
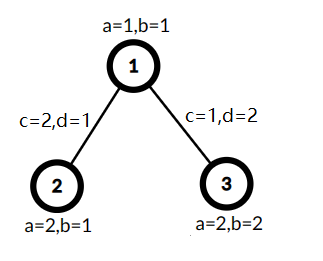 Дерево с тремя вершинами, $$$\min(A,C)=1,B+D=7$$$, стоимость равна $$$7$$$.
Дерево с тремя вершинами, $$$\min(A,C)=1,B+D=7$$$, стоимость равна $$$7$$$. 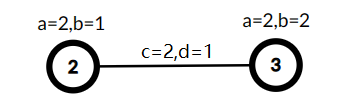 Выбрали вершины $$$2$$$ и $$$3$$$ как $$$S'$$$, использовали ребро $$$(1,2)$$$ с $$$c_j = 2$$$ и $$$d_j = 1$$$, чтобы соединить эти вершины, теперь $$$\min(A,C)=2,B+D=4$$$, стоимость равна $$$8$$$.
Выбрали вершины $$$2$$$ и $$$3$$$ как $$$S'$$$, использовали ребро $$$(1,2)$$$ с $$$c_j = 2$$$ и $$$d_j = 1$$$, чтобы соединить эти вершины, теперь $$$\min(A,C)=2,B+D=4$$$, стоимость равна $$$8$$$. Пусть $$$A$$$ — минимум из значений $$$a_i$$$ в $$$T'$$$, и $$$C$$$ — минимум из значений $$$c_i$$$ в $$$T'$$$. Пусть $$$B$$$ — сумма значений $$$b_i$$$ в $$$T'$$$, и $$$D$$$ — сумма значений $$$d_i$$$ в $$$T'$$$. Определим $$$\min(A, C) \cdot (B + D)$$$ как стоимость $$$T'$$$. Вам нужно найти максимально возможную стоимость $$$T'$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$3\le n \le 2\cdot 10^5$$$) — количество вершин в дереве $$$T$$$.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1\le a_i\le 2\cdot 10^5$$$), где $$$i$$$-е целое число обозначает значение $$$a_i$$$ у $$$i$$$-й вершины.
Третья строка содержит $$$n$$$ целых чисел $$$b_1, b_2, \ldots, b_n$$$ ($$$1\le b_i\le 2\cdot 10^5$$$), где $$$i$$$-е целое число обозначает значение $$$b_i$$$ у $$$i$$$-й вершины.
Далее следует $$$n-1$$$ строка, $$$j$$$-я из которых содержит четыре целых числа $$$x_j,y_j,c_j,d_j$$$ ($$$1\le x_j,y_j\le n,1\le c_j,d_j\le 2\cdot 10^5$$$), представляющих ребро $$$(x_j,y_j)$$$ и его значения $$$c_j$$$ и $$$d_j$$$ соответственно. Гарантируется, что рёбра образуют дерево.
Выведите единственное целое число — максимальное возможную стоимость $$$T'$$$.
3 1 2 2 1 1 2 1 2 2 1 1 3 1 2
8
5 2 4 2 1 1 2 4 4 4 4 2 5 3 3 3 5 2 4 4 2 5 5 5 1 1 5
35
6 5 7 10 7 9 4 6 9 7 9 8 5 2 1 5 1 3 2 2 4 4 3 6 3 5 1 7 4 6 5 6 8
216
5 1000 1000 1 1000 1000 1000 1000 1 1000 1000 1 2 1 1 2 3 1000 1000 3 4 1000 1000 3 5 1000 1000
7000000
Дерево из первого примера изображено в условии.
Дерево из второго примера изображено ниже:
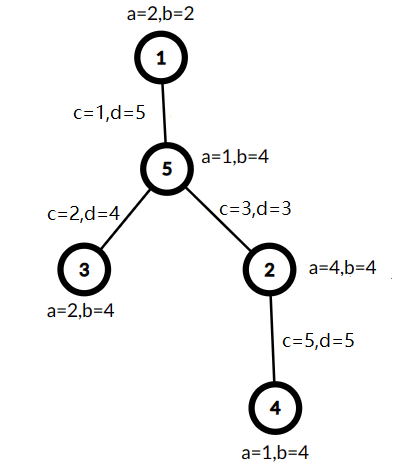
$$$A = 1, B = 18, C = 1, D = 17$$$, поэтому стоимость равна $$$\min(1,1) \cdot (18 + 17) = 35$$$.
| Название |
|---|




