| Codeforces Round 872 (Div. 1) |
|---|
| Закончено |
LuoTianyi дала вам дерево со значениями в вершинах, корнем этого дерева является вершина $$$1$$$.
За одну операцию вы можете изменить значение в любой вершине на любое неотрицательное целое число.
Вам нужно найти минимальное количество операций, которые нужно сделать, чтобы побитовое исключающее ИЛИ на любом пути от корня до листа$$$^{\dagger}$$$ было равно нулю.
$$$^{\dagger}$$$Листом в корневом дереве называется вершина, которая имеет ровно одного соседа, и при этом не является корнем.
Первая строка содержит единственное целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество вершин в дереве.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$), где $$$i$$$-е число равно значению в $$$i$$$-й вершине.
Следующие $$$n−1$$$ строка описывают рёбра дерева. $$$i$$$-я строка содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i,v_i \le n, u_i \neq v_i$$$) — вершины, соединённые ребром дерева. Гарантируется, что данные рёбра образуют дерево.
Выведите единственное целое число — минимальное количество операций.
6 3 5 7 5 8 4 1 2 1 3 1 4 3 5 4 6
3
8 7 10 7 16 19 9 16 11 1 5 4 2 6 5 5 2 7 2 2 3 3 8
3
4 1 2 1 2 1 2 2 3 4 3
0
9 4 3 6 1 5 5 5 2 7 1 2 2 3 4 1 4 5 4 6 4 7 8 1 8 9
2
Дерево из первого примера:
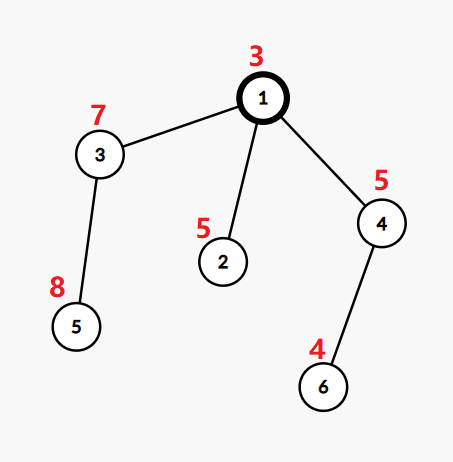
Если мы поменяем значение в вершине $$$2$$$ на $$$3$$$, значение в вершине $$$5$$$ на $$$4$$$, значение в вершине $$$6$$$ на $$$6$$$, то дерево станет подходящим.
Побитовое исключающее ИЛИ от корня до листа $$$2$$$ будет равно $$$3 \oplus 3=0$$$.
Побитовое исключающее ИЛИ от корня до листа $$$5$$$ будет равно $$$4 \oplus 7 \oplus 3=0$$$.
Побитовое исключающее ИЛИ от корня до листа $$$6$$$ будет равно $$$6 \oplus 5 \oplus 3=0$$$.
Дерево из второго примера:
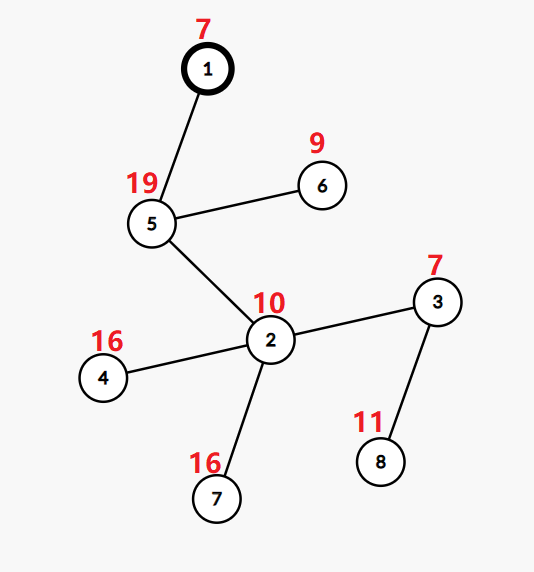
Если мы поменяем значение в вершине $$$2$$$ на $$$4$$$, значение в вершине $$$3$$$ на $$$27$$$, значение в вершине $$$6$$$ на $$$20$$$, то дерево станет подходящим.
Побитовое исключающее ИЛИ от корня до листа $$$6$$$ будет равно $$$20 \oplus 19 \oplus 7=0$$$.
Побитовое исключающее ИЛИ от корня до листа $$$8$$$ будет равно $$$11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0$$$.
Побитовое исключающее ИЛИ от корня до листа $$$4$$$ будет равно $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.
Побитовое исключающее ИЛИ от корня до листа $$$7$$$ будет равно $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.
В третьем примере единственным листом является вершина $$$4$$$, и побитовое исключающее ИЛИ на пути до неё равно $$$1 \oplus 2 \oplus 1 \oplus 2 = 0$$$, поэтому нам не нужно изменять значения.
В четвёртом примере мы можем изменить значение в вершине $$$1$$$ на $$$5$$$, а значение в вершине $$$4$$$ на $$$0$$$.
Здесь $$$\oplus$$$ обозначает операцию побитового исключающего ИЛИ.
| Название |
|---|




