| Codeforces Round 872 (Div. 1) |
|---|
| Закончено |
Это простая версия задачи. Единственное отличие в том, что в этой версии $$$k\le\min(n,3)$$$. Вы можете делать взломы, только если обе версии задачи сданы.
 Chtholly и летающие острова.
Chtholly и летающие острова. LuoTianyi сейчас живёт в мире с $$$n$$$ летающими островами. Летающие острова соединены $$$n-1$$$ ненаправленной воздушной дорогой, и из любого из двух летающих островов можно добраться до другого, путешествуя по воздушным дорогам. Это означает, что $$$n$$$ летающих островов образуют дерево.
Однажды, LuoTianyi захотела встретиться со своими друзьями: Chtholly, Nephren, William, .... Всего она хочет встретиться с $$$k$$$ людьми. Она не знает их точного расположения, но она знает, что они находятся на попарно различных островах. Она называет остров хорошим тогда и только тогда, когда сумма расстояний$$$^{\dagger}$$$ от него до островов с $$$k$$$ людьми минимально возможная среди всех $$$n$$$ островов.
Сейчас LuoTianyi хочет узнать, если $$$k$$$ человек случайным образом находятся в $$$k$$$ различных из $$$n$$$ островов, чему равно математическое ожидание количества хороших островов? Вам нужно сказать ей математическое ожидание по модулю $$$10^9+7$$$.
$$$^{\dagger}$$$Расстоянием между двумя островами называется минимальное количество воздушных дорог, по которым нужно пройти, чтобы перейти с одного острова на другой.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1\le k \le \min(n,3), 1\le n \le 2\cdot 10^5$$$) — количество островов и людей соответственно.
Следующие $$$n−1$$$ строка описывают воздушные дороги. $$$i$$$-я из них содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i,v_i \le n, u_i \neq v_i$$$) — острова, соединённые $$$i$$$-й воздушной дорогой.
Гарантируется, что воздушные дороги образуют дерево.
Выведите единственное целое число — математическое ожидание количества хороших островов по модулю $$$10^9 + 7$$$.
Формально, пусть $$$M = 10^9 + 7$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0$$$ ($$$\operatorname{mod} M$$$). Выведите целое число, равное $$$p \cdot q^{-1}$$$ $$$\operatorname{mod} M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p$$$ ($$$\operatorname{mod} M$$$).
4 2 1 2 2 3 3 4
666666674
5 1 1 2 2 3 3 4 3 5
1
В первом примере дороги образуют следующее дерево:
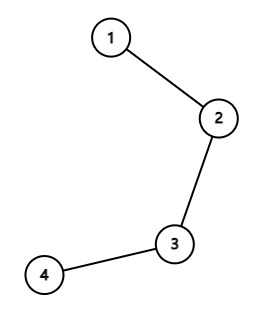
Если люди находятся на островах $$$1$$$ и $$$2$$$, тогда острова $$$1$$$ и $$$2$$$ являются хорошими.
Сумма расстояний от острова $$$1$$$ или $$$2$$$ до всех людей равна $$$1+0=1$$$, что минимально. В это время сумма расстояний от острова $$$3$$$ до всех людей равна $$$2+1=3$$$, что больше $$$1$$$.
Таким же образом, когда люди находятся на островах $$$1$$$ и $$$3$$$, тогда острова $$$1,2$$$ и $$$3$$$ являются хорошими.
Когда люди находятся на островах $$$1$$$ и $$$4$$$, тогда острова $$$1,2,3$$$ и $$$4$$$ являются хорошими.
Когда люди находятся на островах $$$2$$$ и $$$3$$$, тогда острова $$$2$$$ и $$$3$$$ являются хорошими.
Когда люди находятся на островах $$$2$$$ и $$$4$$$, тогда острова $$$2,3$$$ и $$$4$$$ являются хорошими.
Когда люди находятся на островах $$$3$$$ и $$$4$$$, тогда острова $$$3$$$ и $$$4$$$ являются хорошими.
Поэтому математическое ожидание количества хороших островов равно $$$\frac{16}{6}$$$, что равняется $$$666666674$$$ по модулю $$$10^9+7$$$.
Во втором примере воздушные дороги образуют следующее дерево:
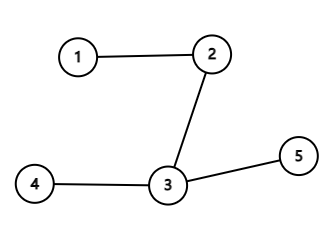
Всегда есть единственный хороший остров, поэтому математическое ожидание равно $$$1$$$.
| Название |
|---|




