C. Лисица и полный обход древа
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Лисица Яэ забралась на древо Священной сакуры. Древом называют связный неориентированный граф, не содержащий циклов.

Для передвижения по древу лисица применяет свои магические способности. Яэ может прыгнуть из вершины $$$v$$$ в другую вершину $$$u$$$ тогда и только тогда, когда расстояние между этими вершинами не превосходит $$$2$$$. Иными словами, за один прыжок Яэ может перепрыгнуть из вершины $$$v$$$ в вершину $$$u$$$, если вершины $$$v$$$ и $$$u$$$ соединены ребром, либо если существует такая вершина $$$w$$$, что вершины $$$v$$$ и $$$w$$$ соединены ребром, а также вершины $$$u$$$ и $$$w$$$ соединены ребром.

После того, как Яэ смогла заполучить лепесток сакуры, она задумалась, существует ли циклический маршрут в древе $$$v_1, v_2, \ldots, v_n$$$, такой что:

  • лисица может совершить прыжок из вершины $$$v_i$$$ в вершину $$$v_{i + 1}$$$,
  • лисица может совершить прыжок из вершины $$$v_n$$$ в вершину $$$v_1$$$,
  • все $$$v_i$$$ попарно различны.

Помогите лисице определить, существует ли требуемый обход.

Входные данные

Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин древа.

Каждая из следующих $$$n - 1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — вершины, соединенные ребром. Гарантируется, что данные ребра задают древо.

Выходные данные

В первой строке выведите «Yes» (без кавычек), если требуемый обход древа существует, либо «No» (без кавычек) в противном случае.

Если требуемый обход древа существует, во второй строке выведите $$$n$$$ целых различных чисел $$$v_1, v_2, \ldots, v_n$$$ ($$$1 \le v_i \le n$$$) — вершины древа в порядке обхода.

Если существует несколько корректных обходов, выведите любой из них.

Примеры
Входные данные
5
1 2
1 3
3 4
3 5
Выходные данные
Yes
4 5 1 2 3
Входные данные
3
1 2
1 3
Выходные данные
Yes
1 2 3
Входные данные
15
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
5 10
5 11
6 12
6 13
7 14
7 15
Выходные данные
No
Примечание

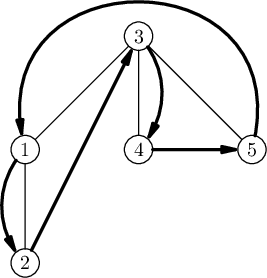
Древо из первого примера изображено ниже. Жирными стрелками обозначен маршрут лисицы.

Во втором примере любая последовательность из трёх различных вершин является корректным маршрутом, потому что лисица может совершить прыжок из любой вершины в любую.

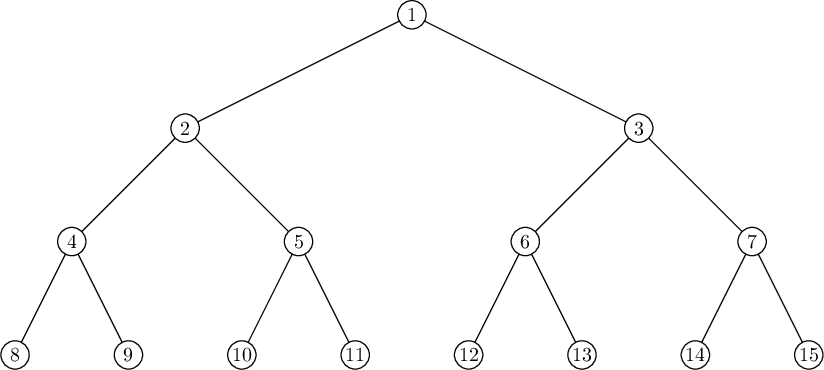
Древо из третьего примера изображено ниже. Можно показать, что для него не существует требуемого маршрута.