| Codeforces Round 862 (Div. 2) |
|---|
| Закончено |
Дано дерево (связный граф без циклов). В каждой вершине дерева записано число. Назовём характеристикой $$$\mathrm{MAD}$$$ (maximum double) дерева максимальное число, которое встречается в вершинах этого дерева хотя бы $$$2$$$ раза. Если же никакое число не встречается в дереве больше одного раза, то положим $$$\mathrm{MAD}=0$$$.
Заметим, что если удалить ребро из дерева, то оно распадётся на два дерева. Вычислим $$$\mathrm{MAD}$$$ в каждом из деревьев и возьмем максимум из этих двух значений. Полученный результат назовем значением удаленного ребра.
Для каждого ребра найдите его значение. Обратите внимание, что мы в действительности не удаляем ребра из дерева, и каждое значение должно быть вычислено независимо.
В первой строке находится одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество вершин в дереве.
Далее в $$$n - 1$$$ строке находятся по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$) — концы рёбер дерева. Гарантируется, что данные ребра образуют дерево.
В последней строке находятся $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — числа, записанные в вершинах.
Для каждого ребра в порядке ввода выведите одно число — максимум из $$$\mathrm{MAD}$$$ двух деревьев, получающихся после удаления из начального дерева данного ребра.
5 1 2 2 3 2 4 1 5 2 1 3 2 1
0 2 1 2
6 1 2 1 3 1 4 4 5 4 6 1 2 3 1 4 5
1 1 0 1 1
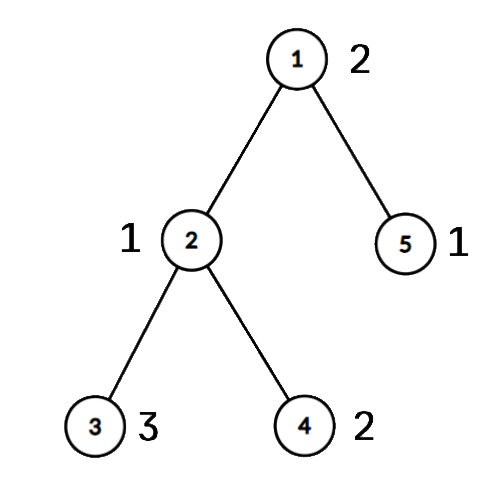
В первом примере после удаления ребра $$$(1, 2)$$$ ни в одном из получившихся поддеревьев никакое число не будет повторяться $$$2$$$ раза, поэтому ответ равен $$$\max(0, 0)=0$$$.
После удаления ребра $$$(2, 3)$$$ в бо́льшем поддереве будет два раза повторяться $$$1$$$ и два раза повторяться $$$2$$$, поэтому $$$\mathrm{MAD}$$$ этого дерева будет равен $$$2$$$.
После удаления ребра $$$(2, 4)$$$ в бо́льшем поддереве будет повторяться только число $$$1$$$, а во втором будет только одно число, поэтому ответом будет $$$1$$$.
Во втором примере, если ребро $$$1 \leftrightarrow 4$$$ не удалено, то в одном из поддеревьев будет две $$$1$$$, поэтому ответ — $$$1$$$. А если удалено ребро $$$1 \leftrightarrow 4$$$, то в обоих поддеревьях нет повторяющихся значений, поэтому ответом будет $$$0$$$.
| Название |
|---|




