| Codeforces Round 857 (Div. 1) |
|---|
| Закончено |
Вася с друзьями хочет разрезать шоколадку, чтобы получилось хотя бы $$$k$$$ кусочков, при этом Вася хочет максимизировать объем наименьшего из них. Резать шоколадку можно только по местам соединения долек, причём каждый разрез должен проходить через всю шоколадку вдоль некоторой гиперплоскости, участвующей в образовании долек. Только сделав все разрезы, Вася разбирает шоколадку на кусочки.
Более формально, Вася хочет выбрать числа $$$b_1, b_2, \dots, b_n$$$ ($$$1 \le b_i \le a_i$$$) — количество частей на которые Вася разрежет шоколадку вдоль каждого измерения. Должно выполняться условие $$$b_1 \cdot b_2 \cdot \ldots \cdot b_n \ge k$$$, чтобы получить не менее $$$k$$$ кусочков после всех разрезаний. Можно заметить, что при оптимальном разрезании с такими параметрами, минимальный кусочек будет содержать $$$\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor$$$ долек, а его объём будет равен $$$\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor \cdot \frac{1}{a_1 a_2 \cdots a_n}$$$.
Вася хочет получить максимальное возможное значение объема минимального кусочка, умноженного на $$$k$$$, то есть он хочет максимизировать число $$$\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor \cdot \frac{1}{a_1 a_2 \cdots a_n} \cdot k$$$. Помогите ему в этом.
В первой строке даны два целых числа $$$n$$$ и $$$k$$$ $$$(1 \le n \le 100$$$, $$$1 \le k \le 10^7)$$$ — размерность шоколадки, и на сколько частей её нужно поделить.
Во второй строке даны $$$n$$$ целых чисел $$$a_1,\ a_2,\ \dots,\ a_n$$$ $$$(1 \le a_i \le 10^7)$$$ — количество кусочков, на которое размечена шоколадка вдоль каждого из измерений.
Выведите одно число — максимальный возможный объём наименьшего из полученных кусочков, умноженный на $$$k$$$, с абсолютной или относительной погрешностью не более $$$10^{-9}$$$.
Если при заданных ограничениях разрезать шоколадку хотя бы на $$$k$$$ кусочков невозможно, выведите $$$0$$$.
1 2 5
0.8
2 6 5 10
0.72
2 7 4 4
0.875
2 3 4 5
0.75
4 444 57 179 239 2
0.97557326850704739751
2 5 2 2
0
В первом примере одномерную шоколадку можно разделить так:

Тогда ответ будет $$$\frac{2}{5} \cdot 2 = 0.8$$$
Во втором примере шоколадку можно разрезать следующим образом:
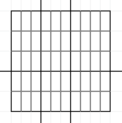
Тогда ответ будет $$$\frac{2}{5} \cdot \frac{3}{10} \cdot 6 = 0.72$$$
В третьем примере шоколадку можно разрезать следующим образом:

Тогда ответ будет $$$\frac{2}{4} \cdot \frac{1}{4} \cdot 7 = 0.875$$$
| Название |
|---|




