| Codeforces Round 860 (Div. 2) |
|---|
| Закончено |
В магазине продаётся $$$n$$$ типов конфет с номерами от $$$1$$$ до $$$n$$$. Одна конфета типа $$$i$$$ стоит $$$b_i$$$ монет. Всего в магазине есть $$$a_i$$$ конфет типа $$$i$$$.
Вам необходимо расфасовать все конфеты по пачкам, каждая пачка должна состоять только из конфет одного типа. Формально, для каждого типа конфет $$$i$$$ вам необходимо выбрать число $$$d_i$$$, обозначающее количество конфет типа $$$i$$$ в одной пачке, так, чтобы $$$a_i$$$ делилось без остатка на $$$d_i$$$.
Тогда стоимость одной пачки конфет типа $$$i$$$ будет равна $$$b_i \cdot d_i$$$. Обозначим эту стоимость за $$$c_i$$$, то есть $$$c_i = b_i \cdot d_i$$$.
После расфасовки пачки конфет будут помещены на полку. Рассмотрим стоимости пачек, расположенных на полке, в порядке $$$c_1, c_2, \ldots, c_n$$$. Для описания стоимостей будут использоваться ценники. Один ценник может описать стоимость всех товаров от $$$l$$$ до $$$r$$$ включительно, если $$$c_l = c_{l+1} = \ldots = c_r$$$. Каждый из товаров от $$$1$$$ до $$$n$$$ должен быть описан хотя бы одним ценником. К примеру, если $$$c_1, \ldots, c_n = [4, 4, 2, 4, 4]$$$, для описания всех товаров будет достаточно $$$3$$$ ценника, первый ценник описывает товары $$$1, 2$$$, второй: $$$3$$$, третий: $$$4, 5$$$.
Вам даны числа $$$a_1, b_1, a_2, b_2, \ldots, a_n, b_n$$$. Ваша задача выбрать числа $$$d_i$$$ так, чтобы $$$a_i$$$ делилось на $$$d_i$$$ для всех $$$i$$$, и необходимое количество ценников для описания стоимостей $$$c_1, c_2, \ldots, c_n$$$ было минимально возможным.
Для лучшего понимания условия ознакомьтесь с иллюстрацией первого набора входных данных первого теста:
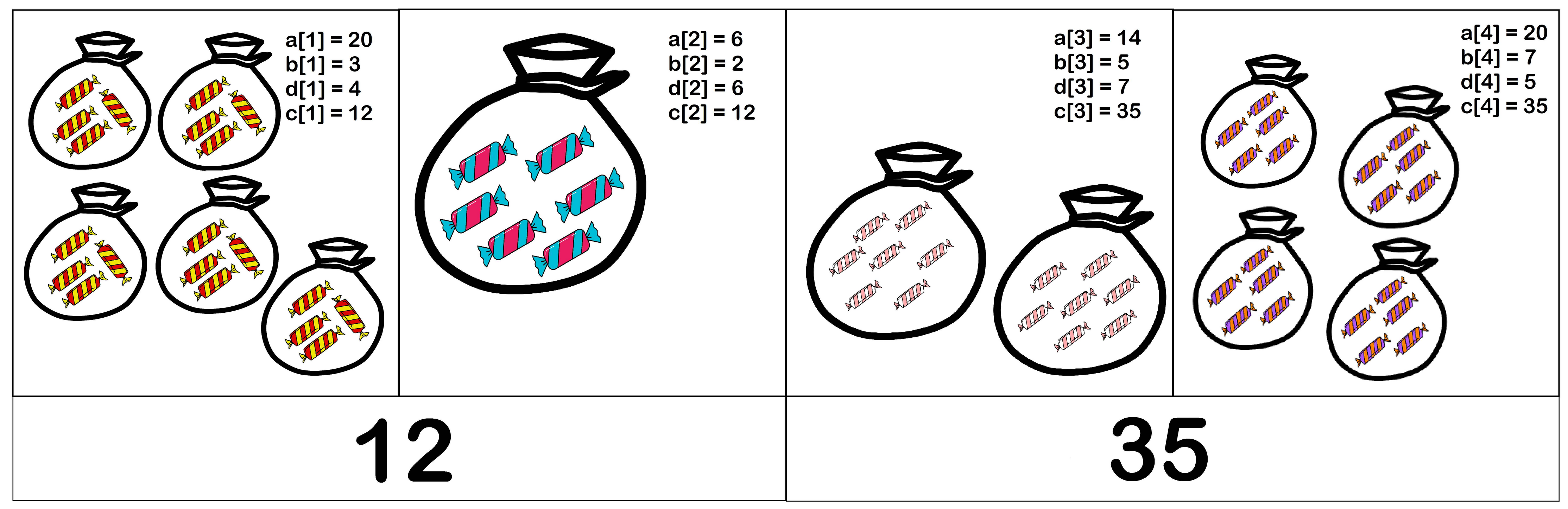
Повторим смысл используемых в задаче обозначений:
$$$a_i$$$ — количество конфет типа $$$i$$$ имеющихся в магазине.
$$$b_i$$$ — стоимость одной конфеты типа $$$i$$$.
$$$d_i$$$ — количество конфет типа $$$i$$$ в одной пачке.
$$$c_i$$$ — стоимость одной пачки конфет типа $$$i$$$, выражается по формуле $$$c_i = b_i \cdot d_i$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 100\,000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 200\,000$$$) — количество видов конфет.
Каждая из следующих $$$n$$$ строк каждого набора входных данных содержит два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i \le 10^9$$$, $$$1 \le b_i \le 10\,000$$$) — количество конфет и стоимость одной конфеты типа $$$i$$$ соответственно.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$200\,000$$$.
Для каждого набора входных данных, выведите минимальное количество ценников необходимое для описания стоимостей всех товаров в магазине.
5420 36 214 520 73444 52002 102020 257 76 515 210 37 7510 111 55 12 28 267 1212 35 39 129 31000000000 10000
2 1 3 2 5
В первом наборе входных данных можно выбрать $$$d_1 = 4$$$, $$$d_2 = 6$$$, $$$d_3 = 7$$$, $$$d_4 = 5$$$. Тогда стоимости товаров будут равны: $$$[12, 12, 35, 35]$$$. Для их описания хватит $$$2$$$ ценников, первый ценник для $$$c_1, c_2$$$ и второй ценник для $$$c_3, c_4$$$. Можно показать, что при любом корректном выборе $$$d_i$$$ для описания всех товаров понадобится как минимум $$$2$$$ ценника. Также обратите внимание, что этот пример иллюстрируется картинкой в условии задачи.
Во втором наборе входных данных при $$$d_1 = 4$$$, $$$d_2 = 2$$$, $$$d_3 = 10$$$ стоимости всех товаров будут равны $$$20$$$. Таким образом $$$1$$$ ценника хватит для описания всех товаров. Обратите внимание, что $$$a_i$$$ делится на $$$d_i$$$ для всех $$$i$$$, что является необходимым условием.
В третьем наборе входных данных нетрудно понять, что для описания $$$2$$$, $$$3$$$ и $$$4$$$ товара может быть использован один ценник. И дополнительно понадобится по ценнику для товаров $$$1$$$ и $$$5$$$. Итого $$$3$$$ ценника.
| Название |
|---|




