| Codeforces Round 864 (Div. 2) |
|---|
| Закончено |
У Li Hua есть дерево из $$$n$$$ вершин и $$$n-1$$$ рёбер. Вершины пронумерованы от $$$1$$$ до $$$n$$$.
Пара вершин $$$(u,v)$$$ ($$$u < v$$$) считается милой, если ровно одно из следующих двух утверждений истинно:
- $$$u$$$ является вершиной с минимальным индексом среди всех вершин на пути $$$(u,v)$$$.
- $$$v$$$ — вершина с максимальным индексом среди всех вершин на пути $$$(u,v)$$$.
Будет выполнено $$$m$$$ операций. В каждой операции Li Hua выбирает целое число $$$k_j$$$, затем вставляет в дерево вершину с номером $$$n+j$$$, соединяющуюся с вершиной номер $$$k_j$$$.
Он хочет подсчитать количество милых пар вершин до операций и после каждой операции.
Предположим, что вы Li Hua. Пожалуйста, решите эту задачу.
Первая строка содержит одно целое число $$$n$$$ ($$$2\le n\le 2\cdot 10^5$$$) — количество вершин в дереве.
Следующие $$$n-1$$$ строк содержат ребра дерева. В $$$i$$$-й строке записаны два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1\le u_i,v_i\le n$$$; $$$u_i\ne v_i$$$) — соответствующее ребро. Данные рёбра образуют дерево.
Следующая строка содержит одно целое число $$$m$$$ ($$$1\le m\le 2\cdot 10^5$$$) — количество операций.
Следующие $$$m$$$ строк содержат операции — по одной операции в строке. В $$$j$$$-й операции содержится одно целое число $$$k_j$$$ ($$$1\le k_j < n+j$$$) — вершина.
Выведите $$$m+1$$$ целых чисел — количество милых пар вершин до операций и после каждой операции.
7 2 1 1 3 1 4 4 6 4 7 6 5 2 5 6
11 15 19
Начальное дерево показано на следующем рисунке:
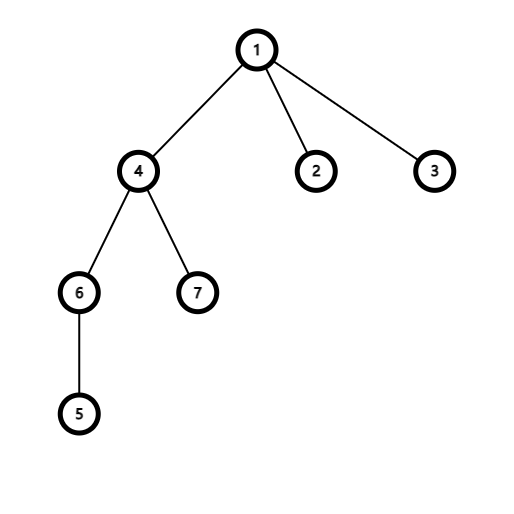 |
Существует $$$11$$$ милых пар — $$$(1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)$$$.
Аналогично, мы можем посчитать милые пары после каждой операции, и результатами будут $$$15$$$ и $$$19$$$.
| Название |
|---|




