| Codeforces Round 864 (Div. 2) |
|---|
| Закончено |
Имеется прямоугольный лабиринт размером $$$n\times m$$$. Обозначим $$$(r,c)$$$ как клетку в $$$r$$$-й строке сверху и $$$c$$$-м столбце слева. Две клетки называются соседними, если они имеют общую сторону. Путь — это последовательность пустых клеток, в которой любые две подряд идущие клетки являются соседними.
Каждая клетка изначально пуста. Li Hua может выбрать несколько клеток (кроме $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$) и поместить в каждую из них препятствие. Он хочет узнать минимальное количество препятствий, которые нужно поставить, чтобы не существовало пути из $$$(x_1, y_1)$$$ в $$$(x_2, y_2)$$$.
Предположим, что вы Li Hua. Пожалуйста, решите эту задачу.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 500$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n,m$$$ ($$$4\le n,m\le 10^9$$$) — размер лабиринта.
Вторая строка каждого набора входных данных содержит четыре целых числа $$$x_1,y_1,x_2,y_2$$$ ($$$1\le x_1,x_2\le n, 1\le y_1,y_2\le m$$$) — координаты начальной и конечной клетки.
Гарантируется, что $$$|x_1-x_2|+|y_1-y_2|\ge 2$$$.
Для каждого набора входных данных выведите минимальное количество препятствий, которое нужно поставить на поле, чтобы не существовало пути из $$$(x_1, y_1)$$$ в $$$(x_2, y_2)$$$.
34 42 2 3 36 71 1 2 39 95 1 3 6
4 2 3
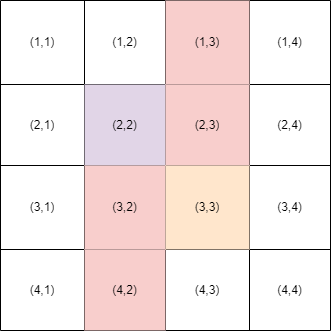
В первом наборе входных данных можно поставить препятствия на $$$(1,3), (2,3), (3,2), (4,2)$$$. Тогда путь из $$$(2,2)$$$ в $$$(3,3)$$$ не будет существовать.
 |
| Название |
|---|




