Дан неориентированный граф из $$$n$$$ вершин и $$$n$$$ ребер, при этом $$$n$$$ делится на $$$6$$$. У каждого ребра есть вес — положительное целое число.
Структура графа имеет следующий вид: граф разделен на $$$\frac{n}{3}$$$ троек вершин, в первую тройку входят вершины $$$1, 2, 3$$$, во вторую — $$$4, 5, 6$$$, и так далее. Каждая пара вершин из одной и той же тройки соединена ребром. Ни одно ребро не соединяет две вершины из разных троек.
Вершины этого графа надо раскрасить в два цвета, красный и синий. Каждая вершина должна быть покрашена в один из цветов; ровно $$$\frac{n}{2}$$$ вершин должно быть покрашено в красный, и ровно $$$\frac{n}{2}$$$ — в синий. Раскраски, отвечающие этим условиям, будем называть валидными.
Вес раскраски — это суммарный вес всех ребер, соединяющих вершины разных цветов.
Пусть $$$W$$$ — максимальный вес валидной раскраски. Посчитайте количество валидных раскрасок с весом $$$W$$$ и выведите результат по модулю $$$998244353$$$.
В первой строке задано одно целое число $$$n$$$ ($$$6 \le n \le 3 \cdot 10^5$$$, $$$n$$$ делится на $$$6$$$).
Во второй строке заданы $$$n$$$ целых чисел $$$w_1, w_2, \dots, w_n$$$ ($$$1 \le w_i \le 1000$$$) — веса ребер. Ребро $$$1$$$ соединяет вершины $$$1$$$ и $$$2$$$, ребро $$$2$$$ соединяет вершины $$$1$$$ и $$$3$$$, ребро $$$3$$$ соединяет вершины $$$2$$$ и $$$3$$$, ребро $$$4$$$ соединяет вершины $$$4$$$ и $$$5$$$, ребро $$$5$$$ соединяет вершины $$$4$$$ и $$$6$$$, ребро $$$6$$$ соединяет вершины $$$5$$$ и $$$6$$$, и так далее.
Выведите одно целое число — количество валидных раскрасок с максимальным весом, взятое по модулю $$$998244353$$$.
12 1 3 3 7 8 5 2 2 2 2 4 2
36
6 4 2 6 6 6 4
2
На картинке изображен граф из первого теста.
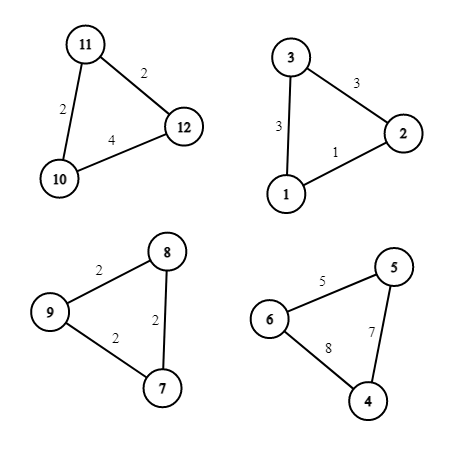
Максимальный вес валидной раскраски этого графа равен $$$31$$$.
| Название |
|---|




