| Codeforces Round 856 (Div. 2) |
|---|
| Закончено |
Вам задано невзвешенное дерево из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$, и список из $$$n-1$$$ целого числа $$$a_1, a_2, \ldots, a_{n-1}$$$. Дерево — это связный неориентированный граф без циклов. Вы можете использовать каждый элемент списка, чтобы пометить одну из вершин дерева. Никакая вершина не должна быть помечена дважды. Вы можете пометить единственную оставшуюся непомеченной вершину любым целым числом.
Вершина $$$x$$$ называется хорошей, если можно так пометить вершины, чтобы для каждой вершины $$$i$$$ ее метка была равна расстоянию между $$$x$$$ и $$$i$$$. Расстояние между двумя вершинами $$$s$$$ и $$$t$$$ на дереве — это минимальное количество ребер на пути, который начинается в вершине $$$s$$$ и заканчивается в вершине $$$t$$$.
Найдите все хорошие вершины.
Первая строка содержит одно целое число $$$n$$$ ($$$2\le n\le 2\cdot 10^5$$$) — число вершин в дереве.
Вторая строка содержит $$$n - 1$$$ целое число $$$a_1,a_2,\ldots,a_{n-1}$$$ ($$$0\le a_i < n$$$) — заданный список.
Затем следуют $$$n−1$$$ строк. Каждая из них содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1\le u,v\le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что ребра образуют дерево.
В первой строке выведите количество хороших вершин.
Во второй строке выведите номера всех хороших вершин в порядке возрастания.
6 2 1 0 1 2 1 2 2 3 2 4 4 5 4 6
2 2 4
5 1 2 1 2 1 2 3 2 3 4 5 4
1 3
3 2 2 1 2 2 3
0
На рисунке ниже показано дерево для первого примера:
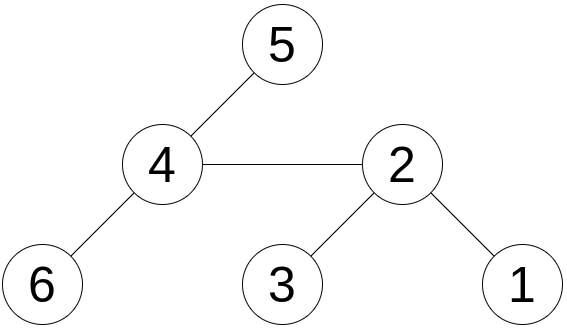
На рисунке ниже показаны две возможные разметки, такие что $$$2$$$ — хорошая вершина (слева) и $$$4$$$ — хорошая вершина (справа).
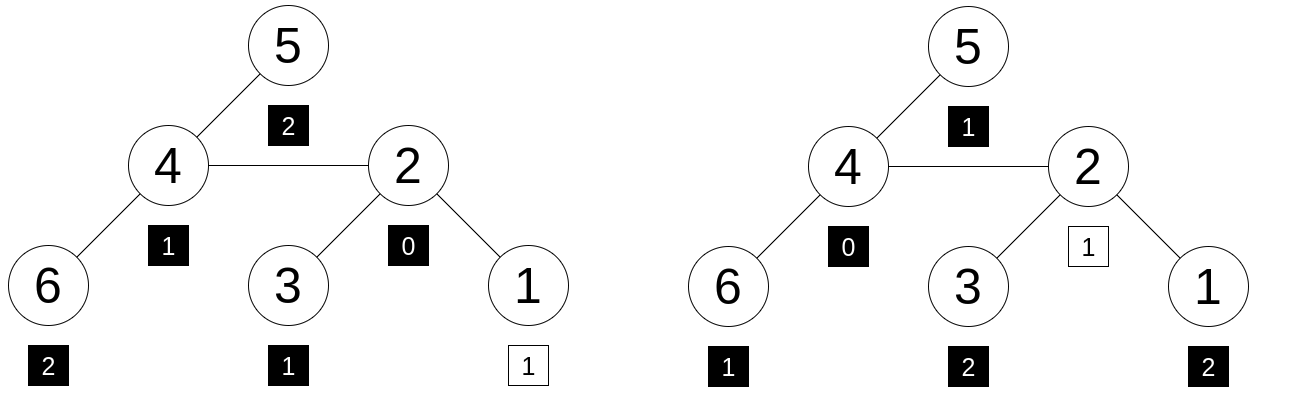
Квадрат под каждой вершиной означает ее метку. Черные квадраты содержат числа, которые были в данном списке, а единственный белый квадрат содержит единственное число, которого не было в данном списке.
Во втором примере единственной хорошей вершиной является вершина $$$3$$$.
В третьем примере хороших вершин нет.
| Название |
|---|




